
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
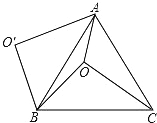
①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;
②连接OO′,则OO′=4;
③∠AOB=150°;
④S四边形AOBO′=6+4![]() .
.
其中正确的结论是 .
【答案】①②③④
【解析】
试题解析:如图,连接OO′;
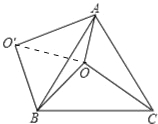
∵△ABC为等边三角形,
∴∠ABC=60°,AB=CB;
由题意得:∠OBO′=60°,OB=O′B,
∴△OBO′为等边三角形,∠ABO′=∠CBO,
∴OO′=OB=4;∠BOO′=60°,
∴选项②正确;
在△ABO′与△CBO中,
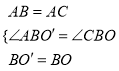 ,
,
∴△ABO′≌△CBO(SAS),
∴AO′=OC=5,
△BO′A可以由△BOC绕点B逆时针方向旋转60°得到,
∴选项①正确;
在△AOO′中,∵32+42=52,
∴△AOO′为直角三角形,
∴∠AOO′=90°,∠AOB=90°+60°=150°,
∴选项③正确;
∵S四边形AOBO′=![]() ,
,
∴选项④正确.
综上所述,正确选项为①②③④.


科目:初中数学 来源: 题型:
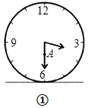
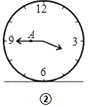
【题目】图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点![]() ,当钟面显示3点30分时,分针垂直于桌面,点
,当钟面显示3点30分时,分针垂直于桌面,点![]() 距离桌面的高度为
距离桌面的高度为![]() 公分,图②表示钟面显示3点45时,点
公分,图②表示钟面显示3点45时,点![]() 距桌面的高度为
距桌面的高度为![]() 公分,若钟面显示3点55时,点
公分,若钟面显示3点55时,点![]() 距离桌面的高度为__________公分.
距离桌面的高度为__________公分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
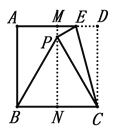
查看答案和解析>>
科目:初中数学 来源: 题型:
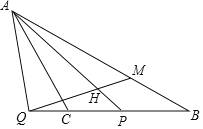
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
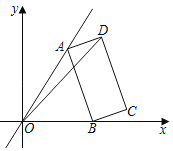
【题目】如图,在平面直角坐标系中,点A在一次函数y=![]() x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2
x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2![]() ,AD=1,则OD的最大值是( )
,AD=1,则OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠ACB=90°,点D为AB上一点.
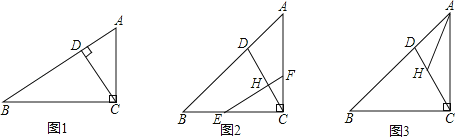
(1)如图1,若CD⊥AB,求证:CD2=ADDB;
(2)如图2,若AC=BC,EF⊥CD于H,EF与BC交于E,与AC交于F,且![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)如图3,若AC=BC,点H在CD上,且∠AHD=45°,CH=3DH,直接写出tan∠ACH的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD的边AD的延长线上截取DE=AD,F是AE延长线上的一点,连结BD、CE、BF分别交CE、CD于G、H.
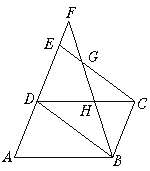
求证:(1)△ABD≌△DCE;
(2)CE∶CG=DF∶AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数y=x+![]() 的图象和性质.
的图象和性质.
小华根据学习函数的方法和经验,进行了如下探究,下面是小华的探究过程,请补充完整:
(1)函数的自变量x的取值范围是:____;
(2)如表是y与x的几组对应值,请将表格补充完整:
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
(3)如图,在平面直角坐标系中描点并画出此函数的图象;
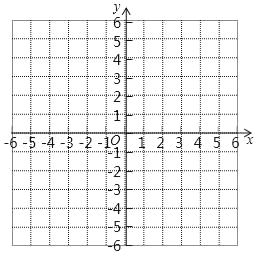
(4)进一步探究:结合函数的图象,写出此函数的性质(一条即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com