
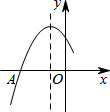
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:分析 ①根据抛物线与x轴交点个数可判断;②根据抛物线对称轴可判断;③根据抛物线与x轴的另一个交点坐标可判断;④根据B、C两点离对称轴的距离的大小,可判断.
解答 解:由函数图象可知抛物线与x轴有2个交点,
∴b2-4ac>0即b2>4ac,故①正确;
∵对称轴为直线x=-1,
∴-$\frac{b}{2a}$=-1,即2a-b=0,故②错误;
∵抛物线与x轴的交点A坐标为(-3,0)且对称轴为x=-1,
∴抛物线与x轴的另一交点为(1,0),
∴将(1,0)代入解析式可得,a+b+c=0,故③错误;
由|-$\frac{5}{2}$+1|>|-$\frac{1}{2}$+1|,可知点B离对称轴距离较远,
∴y1<y2,故④正确;
综上,正确的结论是:①④,
故答案为①④.
点评 本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c(a≠0),a的符号由抛物线开口方向决定;b的符号由对称轴的位置及a的符号决定;c的符号由抛物线与y轴交点的位置决定;抛物线与x轴的交点个数,决定了b2-4ac的符号,此外还要注意x=1,-3对应函数值的正负来判断其式子的正确与否.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com