
分析 原式括号中两项通分并利用同分母分式的减法法则计算,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:$\frac{2}{{x}^{2}-1}$-$\frac{1}{x-1}$,
=$\frac{2}{(x+1)(x-1)}$-$\frac{x+1}{(x+1)(x-1)}$,
=$\frac{1-x}{(x+1)(x-1)}$,
=-$\frac{1}{x+1}$.
当x=tan60°-1即x=$\sqrt{3}$-1时,原式=-$\frac{1}{\sqrt{3}-1+1}$=-$\frac{1}{\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,特殊角的三角函数值,熟练掌握运算法则是解本题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
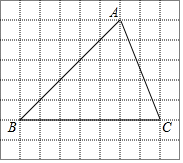 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
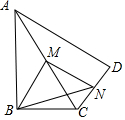 如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC平分∠BAD,AC=AD,M,N分别为AC,CD的中点,AM=1,连接MN,BN,则BN的长为$\sqrt{2}$.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC平分∠BAD,AC=AD,M,N分别为AC,CD的中点,AM=1,连接MN,BN,则BN的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com