
分析 (1)设甲、乙两车每趟的运费分别为m元、n元,根据:①甲车费用-乙车费用=200,②12×(甲车费用+乙车费用)=4800,列方程组求解可得;
(2)设单独租用甲车运完此批货物需运a趟,则乙车运完此批货物需运2a趟,记这批货物的总量为1,根据:12×(甲车每趟运送量+乙车每趟运送量)=1,列分式方程求解即可;
(3)先根据:甲车x趟的运送量+乙车y趟的运送量=1可得y关于x的函数关系,再根据:总运费=甲车的总运费+乙车的总运费,列出W关于x的函数关系,由一次函数的性质可得W的最值情况.
解答 解:(1)设甲、乙两车每趟的运费分别为m元、n元,
根据题意得:$\left\{\begin{array}{l}{m-n=200}\\{12(m+n)=4800}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=300}\\{n=100}\end{array}\right.$,
答:甲、乙两车每趟的运费分别为300元、100元.
(2)设单独租用甲车运完此批货物需运a趟,则乙车运完此批货物需运2a趟.
根据题意得:12($\frac{1}{a}$+$\frac{1}{2a}$)=1
解得:a=18.
经检验a=18是原方程的解,
答:单独租用甲车运完此批货物需运18趟.
(3)由题意得:$\frac{x}{18}$+$\frac{y}{36}$=1,
∴y=36-2x
则W=300x+100y
=300x+100(36-2x)
=100x+3600(0<x<18).
∵100>0,
∴W随着x的增大而增大.
当x=1时,w有最小值,w的最小值为3700元.
点评 本题主要考查二元一次方程组、分式方程、一次函数的应用,理解题意抽象出相等关系列出方程组、方程及一次函数关系是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
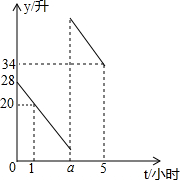 张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
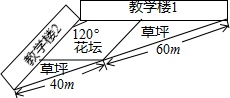 学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.
学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
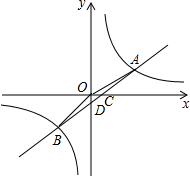 已知:如图所示,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$y=\frac{k}{x}(k≠0)$的图象交于一、三象限内的A、B两点,与x交于点C,与y轴交于点D,OC=1,BC=5,$sin∠BCO=\frac{3}{5}$.
已知:如图所示,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$y=\frac{k}{x}(k≠0)$的图象交于一、三象限内的A、B两点,与x交于点C,与y轴交于点D,OC=1,BC=5,$sin∠BCO=\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com