
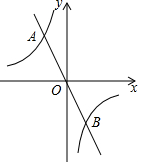
 如图,在平面直角坐标系中,点A是第二象限内双曲线y=-$\frac{2}{x}$上一点,直线AO与双曲线的另一个交点为B.
如图,在平面直角坐标系中,点A是第二象限内双曲线y=-$\frac{2}{x}$上一点,直线AO与双曲线的另一个交点为B.分析 (1)作AC⊥x轴于C,运用勾股定理求得AO的长,即可得到AB的长;
(2)当AB为第二、四象限角平分线时,AB的长最小,设A(-x,x),代入双曲线y=-$\frac{2}{x}$可得点A的坐标为(-$\sqrt{2}$,$\sqrt{2}$).
解答 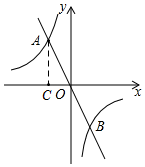 解:(1)如图,作AC⊥x轴于C,
解:(1)如图,作AC⊥x轴于C,
∵点A的坐标为(-1,2),
∴OC=1,AC=2,
∴Rt△AOC中,AO=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
由点A与点B关于原点成中心对称,可得OB=OA=$\sqrt{5}$,
∴AB=2$\sqrt{5}$;
(2)当AB为第二、四象限角平分线时,AB的长最小,
此时,可设A(-x,x),代入双曲线y=-$\frac{2}{x}$可得,-x2=-2,
解得x=$\sqrt{2}$,
∴点A的坐标为(-$\sqrt{2}$,$\sqrt{2}$).
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与正比例函数交点关于原点成中心对称.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.
如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 实践操作
实践操作查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com