
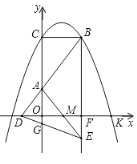
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
【答案】(1)BC=m;(2)点D在抛物线上,理由见解析; (3)![]() .
.
【解析】
(1)先求出抛物线的对称轴,然后根据点C与点B关于对称轴对称即可求出BC的长;
(2)根据题意即可求出BC和二次函数解析式,根据利用平行证出△AOD∽△ACB,列出比例式即可求出点D的坐标,最后代入解析式即可判断结论;
(3)根据已知条件可得点E的坐标为(m,![]() ),即OF=m,EF=
),即OF=m,EF=![]() ,△ODG∽△FDE,然后用m表示出OD、DF、OG、MF和OM,再利用平行证出△AOM∽△EFM,列出比例式即可求出m的值,从而求出结论.
,△ODG∽△FDE,然后用m表示出OD、DF、OG、MF和OM,再利用平行证出△AOM∽△EFM,列出比例式即可求出m的值,从而求出结论.
解:(1)![]() 图象的对称轴为直线x=
图象的对称轴为直线x=![]() ,点C与点B关于对称轴对称
,点C与点B关于对称轴对称
∴BC=![]() =m;
=m;
(2)在,理由如下
当m=2时,BC=2,![]()
∵![]() ,
,![]()
∴△AOD∽△ACB
∴![]()
∴OD=![]() BC=1
BC=1
∴点D的坐标为(-1,0)
当x=-1时,![]()
∴点D在抛物线.
(3)∵![]() ,
,![]()
∴点E的坐标为(m,![]() ),即OF=m,EF=
),即OF=m,EF=![]() ,△ODG∽△FDE
,△ODG∽△FDE
由(2)可知![]()
∴OD=![]() BC=
BC=![]() m,OA=
m,OA=![]() OC
OC
∴DF=OD+OF=![]() m
m
∴![]()
即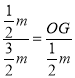
解得:OG=![]() m
m
∵![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]()
∴![]() EF·MF=2×
EF·MF=2×![]() OD·OG
OD·OG
即![]() ·
·![]() ·MF=2×
·MF=2×![]() ·
·![]() m·
m·![]() m
m
解得:MF=![]() m
m
∴OM=OF-MF=![]() m
m
将x=0代入![]() 中,解得y=3
中,解得y=3
∴OC=3
∴OA=1
∵OA∥EF
∴△AOM∽△EFM
∴![]()
即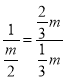
解得:m=1
∴抛物线的解析式为![]()


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设等边三角形的内切圆半径为![]() 外接圆半径为
外接圆半径为![]() ,平面内任意一点
,平面内任意一点![]() 到等边三角形中心的距离为
到等边三角形中心的距离为![]() 若满足
若满足![]() 则称点
则称点![]() 叫做等边三角形的中心关联点.在平面直角坐标系
叫做等边三角形的中心关联点.在平面直角坐标系![]() 中,等边
中,等边![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() .
.
(1)①等边![]() 中心的坐标为 ;
中心的坐标为 ;
②已知点![]() 在
在![]() 中,是等边
中,是等边![]() 的中心关联点的是 ;
的中心关联点的是 ;
(2)如图1,过点![]() 作直线交
作直线交![]() 轴正半轴于
轴正半轴于![]() 使
使![]() .
.
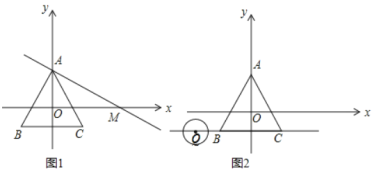
①若线段![]() 上存在等边
上存在等边![]() 的中心关联点
的中心关联点![]() 求
求![]() 的取值范围;
的取值范围;
②将直线![]() 向下平移得到直线
向下平移得到直线![]() 当
当![]() 满足什么条件时,直线
满足什么条件时,直线![]() 上总存在等边
上总存在等边![]() 的中心关联点;
的中心关联点;
(3)如图2,点![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 的半径为
的半径为![]() 当
当![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右移动,运动时间为
个单位的速度向右移动,运动时间为![]() 秒.是否存在某一时刻
秒.是否存在某一时刻![]() 使得
使得![]() 上所有点都是等边
上所有点都是等边![]() 的中心关联点?如果存在,请直接写出所有符合题意的
的中心关联点?如果存在,请直接写出所有符合题意的![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师和学生一起去测量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡比为iFC=1:10(即EF:CE=1:10),学生小明站在离升旗台水平距离为35m(即CE=35m)处的C点,测得旗杆顶端B的仰角为α,已知tanα=![]() ,升旗台高AF=1m,小明身高CD=1.6m,请帮小明计算出旗杆AB的高度.
,升旗台高AF=1m,小明身高CD=1.6m,请帮小明计算出旗杆AB的高度.
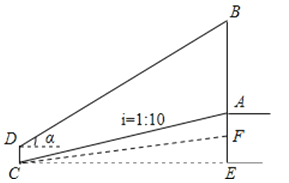
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“危险废物”,处理不当将污染环境,危害健康某市药监部门为了解家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
(1)下列选取样本的方法最合理的一种是 (只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下图:
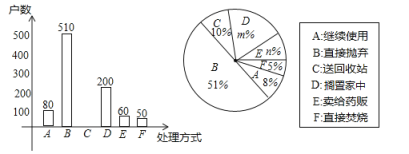
①![]() ,
,
②补全条形统计图;(标上数据)
③家庭过期药品的正确处理方式是送回收站,若该市有![]() 万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
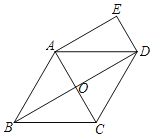
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中学生对待学习的态度一直是教育工作者极为关注的一个问题.为此某市教育局对本市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:喜欢;B级:不太喜欢;C级:不喜欢),并将调查结果绘制成不完整的统计图(如图![]() ).请根据图中提供的信息,解答下列问题:
).请根据图中提供的信息,解答下列问题:
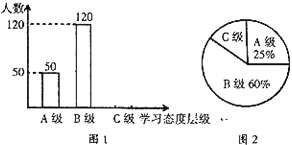
(1)此次抽样调查中,共调查了_____名学生;
(2)将条形统计图补充完整;
(3)求出扇形统计图中![]() 级所占的圆心角的度数;
级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近![]() 名初中生中大约有多少名学生学习态度达标.(达标包括
名初中生中大约有多少名学生学习态度达标.(达标包括![]() 级和
级和![]() 级)
级)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是直线
是直线![]() 上的两点,直线l1、l2的初始位置与直线
上的两点,直线l1、l2的初始位置与直线![]() 重合将l1绕点
重合将l1绕点![]() 顺时针以每秒10°的速度旋转,将l2绕点B逆时针以每秒5°的速度旋转,且两条直线从重合位置同时开始旋转,设旋转时间为
顺时针以每秒10°的速度旋转,将l2绕点B逆时针以每秒5°的速度旋转,且两条直线从重合位置同时开始旋转,设旋转时间为![]() 秒(
秒(![]() 是正整数).当
是正整数).当![]() 时,设
时,设![]() 的交点为
的交点为![]() ;当
;当![]() 时,设
时,设![]() 的交点为
的交点为![]() ;当
;当![]() 时设
时设![]() 的交点为
的交点为![]() ……那么当
……那么当![]() 时,
时, ![]() 相交所得的钝角是__________.当
相交所得的钝角是__________.当![]() 落在
落在![]() 上方时,
上方时, ![]() 的最小值是__________.
的最小值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 是等圆,
是等圆,![]() 内接于
内接于![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.如图,
上.如图,
①以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
下面有四个结论:
①![]()
②![]()
③![]()
④![]()
所有正确结论的序号是( ).
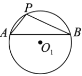
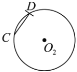
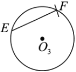
A.①②③④B.①②③C.②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com