
分析 (1)原式先计算除法运算,再计算加减运算即可得到结果;
(2)原式利用加减法则计算即可得到结果;
(3)原式先计算乘除运算,再计算加减运算即可得到结果;
(4)原式利用乘法分配律计算即可得到结果;
(5)原式先计算乘除运算,再计算加减运算即可得到结果;
(6)原式约分即可得到结果;
(7)原式利用乘方的意义计算即可得到结果;
(8)原式利用乘方的意义计算即可得到结果.
解答 解:(1)原式=-12+$\frac{9}{2}$=-7$\frac{1}{2}$;
(2)原式=-1+$\frac{1}{5}$=-$\frac{4}{5}$;
(3)原式=-12+2-5=-15;
(4)原式=1+2-$\frac{8}{3}$+$\frac{2}{3}$=1;
(5)原式=-32-6=-38;
(6)原式=-$\frac{1}{5}$;
(7)原式=-1000;
(8)原式=-4.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
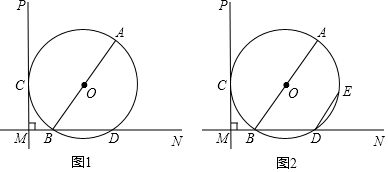
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
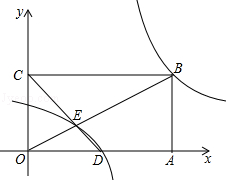 我们规定:函数y=$\frac{ax+k}{x+b}$(a、b、k是常数,k≠ab)叫广义反比例函数.当a=b=0时,广义反比例函数y=$\frac{ax+k}{x+b}$就是反比例函数y=$\frac{k}{x}$(k是常数,k≠0).
我们规定:函数y=$\frac{ax+k}{x+b}$(a、b、k是常数,k≠ab)叫广义反比例函数.当a=b=0时,广义反比例函数y=$\frac{ax+k}{x+b}$就是反比例函数y=$\frac{k}{x}$(k是常数,k≠0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
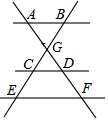 如图.AB∥CD∥EF,AF、BE交于点G,下列比例式错误的是( )
如图.AB∥CD∥EF,AF、BE交于点G,下列比例式错误的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{AG}{GD}=\frac{BG}{CG}$ | C. | $\frac{GC}{GE}=\frac{CD}{EF}$ | D. | $\frac{AB}{EF}=\frac{AG}{GE}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com