
【题目】综合题
(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值
②求:24m﹣6n的值
(2)已知2×8x×16=223 , 求x的值.
【答案】
(1)解:∵4m=a,8n=b,
∴22m=a,23n=b,
22m+3n=22m23n=ab;
②24m﹣6n=24m÷26n=(22m)2÷(23n)2= ![]()
(2)解∵2×8x×16=223,
∴2×(23)x×24=223,
∴2×23x×24=223,
∴1+3x+4=23,
解得:x=6:
【解析】(1)分别将4m , 8n化为底数为2的形式,然后代入①②求解;(2)将8x化为23x , 将16化为24 , 列出方程求出x的值.
【考点精析】本题主要考查了同底数幂的除法的相关知识点,需要掌握同底数幂的除法法则:am÷an=am-n(a≠0,m,n都是正整数,且m>n)才能正确解答此题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b﹣a)
a(b﹣a)
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量.若设原来每天能生产x辆,则可列关于x的不等式为( )
A. 15x>20(x+6) B. 15(x+6)≥20x C. 15x>20( x-6) D. 15(x+6)>20x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E,F.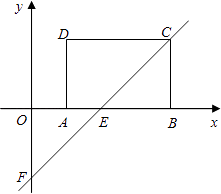
(1)求矩形ABCD的顶点A,B,C,D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x﹣2上一点,若S△POE=5,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB,CD内部,∠B=50°,∠D=30°,求∠BPD. 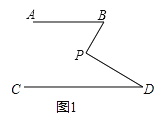
(2)如图2,将点P移到AB,CD外部,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论. 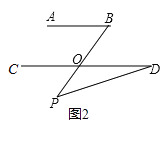
(3)如图3,写出∠BPD,∠B,∠D,∠BQD之间的数量关系?(不需证明) 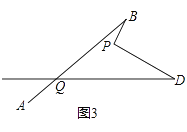
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数. 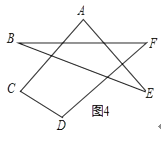
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线 y=x2+1 向右平移 2 个单位,再向上平移 3 个单位后,抛物线的解析式为( )
A. y=(x+2)2+4B. y=(x﹣2)2﹣4
C. y=(x﹣2)2+4D. y=(x+2)2﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com