
【题目】如图,已知四边形AECF是平行四边形,D,B分别在AF,CE的延长线上,连接AB,CD,且∠B=∠D.
求证:(1)△ABE≌△CDF;
(2)四边形ABCD是平行四边形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行四边形的性质得到∠AEC=∠AFC,AE=CF,根据全等三角形的判定定理即可得到结论;
(2)由全等三角形的性质得到AB=CD,BE=DF,根据平行四边形的判定定理即可得到结论.
证明:(1)∵四边形AECF是平行四边形,
∴∠AEC=∠AFC,AE=CF,AF=CE,
∵∠AEC+∠AEB=180°,∠AFC+∠CFD=180°,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
 ,
,
∴△ABE≌△CDF(AAS);
(2)由(1)知△ABE≌△CDF
可得:AB=CD,BE=DF.
∵AF=CE,
∴AF+DF=CE+BE,
∴AF+DF=CE+BE,
即AD=BC,
∴四边形ABCD是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时.
(3)B出发后_____小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB、AC于点D、E,则以下AE与CE的数量关系正确的是( )

A.AE=![]() CEB.AE=
CEB.AE=![]() CEC.AE=
CEC.AE=![]() CED.AE=2CE
CED.AE=2CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF![]() AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.
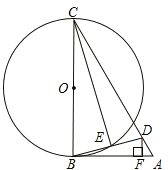
(1)求证:AB是☉O的切线;
(2)若∠A=60°,DF=![]() ,求☉O的直径BC的长。
,求☉O的直径BC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
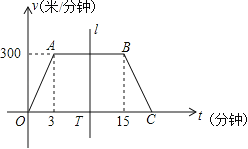
(1)①当t=2分钟时,速度v= 米/分钟,路程s= 米;
②当t=15分钟时,速度v= 米/分钟,路程s= 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式;
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
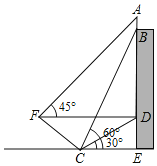
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年初,一场突如其来的疫情,让本该回到学校的学子们宅在家里上网课.为了解学生对网课的满意度,某校随机抽取了部分学生进行调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整),请根据图中信息回答问题:

(1)求被随机抽取的学生数及m的值,并补全条形统计图.
(2)在扇形统计图中,求满意度为“非常不满意”所对应的扇形圆心角的度数.
(3)若该校共有学生3000人,估计上网课满意度为“非常满意”和“满意”的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com