
【题目】如图,在四边形![]() 中,
中, ![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.

(![]() )求证:
)求证: ![]() .
.
(![]() )若
)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)首先由直接三角形的斜边上的中线的性质得出AM=CM,进一步利用等腰三角形的三线合一得出结论;
(2)由直接三角形的斜边上的中线的性质得出AM=MD=MC,利用三角形的内角和得出∠AMD=180°-2∠ADM,∠CMD=180°-2∠CDM,求得∠AMC,进一步利用等腰三角形的性质得出答案即可.
试题解析:
(![]() )证明:∵M为BD中点,
)证明:∵M为BD中点,
在Rt△ABD中,AM=![]() BD,
BD,
在Rt△BCD中,CM=![]() BD,
BD,
∴AM=CM,
∴△AMC为等腰三角形,
∵N为AC中点,
∴MN⊥AC.
(![]() )解:∵M是BD的中点,
)解:∵M是BD的中点,
∴MD=![]() BD,
BD,
∴AM=DM,
∴∠AMD=180°-2∠ADM,
同理∠CMD=180°-2∠CDM,
∴∠AMC=∠AMD+∠CMD=180°-2∠ADM+180°-2∠CDM=120°,
∵AM=DM,
∴∠1=∠2=30°.


科目:初中数学 来源: 题型:
【题目】某生态示范村种植基地计划用90亩~120亩(含90亩与120亩)的土地种植一批葡萄,原计划总产量要达到36万斤.设原计划种植亩数y(亩)、平均亩产量x(万斤)
(1)列出y(亩)与x(万斤)之间的函数关系式,并求自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
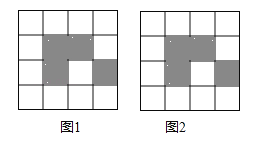
【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
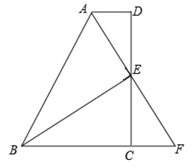
【题目】如图,在四边形 ABCD 中,AD∥BC,E 为 CD 的中点,连接 AE、BE,延长 AE 交 BC 的 延长线于点 F.
(1)△DAE 和△CFE 全等吗?说明理由;
(2)若 AB=BC+AD,说明 BE⊥AF;
(3)在(2)的条件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距离?如果能 请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式x3﹣3xy2﹣4的常数是a,次数是b.
(1)则a=_____,b=_____;并将这两数在数轴上所对应的点A、B表示出来;
(2)数轴上在B点右边有一点C到A、B两点的距离之和为11,求点C在数轴上所对应的数;
(3)在数轴上是否存在点P,使P到A、B、C的距离和等于12?若存在,求点P对应的数;若不存在,请说明理由.
(4)在数轴上是否存在点P,使P到A、B、C的距离和最小?若存在,求该最小值,并求此时P点对应的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
频数 | 16 | 25 | 9 | 7 | 3 |
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几(精确到0.1%)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com