
 ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ�Ҳ�����ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ�Ҳ�����ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
| 2 |
| 3 |
| 2 |
| 3 |
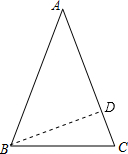
| 3 |
| 5 |
| BD |
| AB |
| (5x)2-(3x)2 |
| BD2+DC2 |
| (3x)2+x2 |
| 10 |
| BC |
| AB |
| ||
| 5 |
| AB2-BD2 |
| 1-k2 |
| 1-k2 |
| BD2+DC2 |
2-2
|
| BC |
| AB |
2-2
|
2-2
|


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
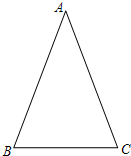 ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת����
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת����| �ױ� |
| �� |
| BC |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.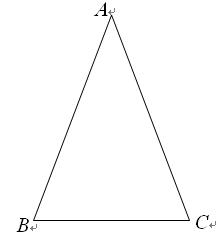
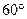 ��ֵΪ�� ��
��ֵΪ�� ��A�� | B��1 | C��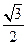 | D��2 |
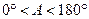 ����A������ֵsad A��ȡֵ��Χ�� .
����A������ֵsad A��ȡֵ��Χ�� .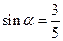 ������
������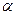 Ϊ��ǣ�����sad
Ϊ��ǣ�����sad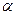 ��ֵ.
��ֵ.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012���㽭��̨��Ƭ���������꼶���Ĵ�ģ�⿼����ѧ�Ծ����������� ���ͣ������
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.���Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad��.��ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA ����ʱsadA=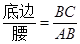 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����. �����������ڽǵ����Զ��壬����������⣺
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����. �����������ڽǵ����Զ��壬����������⣺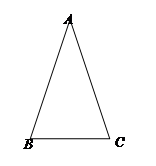
��С��1��sad ��ֵΪ�� �� ��
��ֵΪ�� �� ��
A��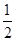 | B��1 | C��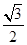 | D��2 |
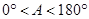 ����A������ֵsadA��ȡֵ��Χ��( �� )
����A������ֵsadA��ȡֵ��Χ��( �� )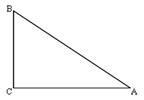
A��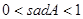 | B��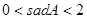 | C��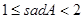 |
D��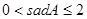 |
 ��AB=25����sadA��ֵ
��AB=25����sadA��ֵ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���Ͼ����������п���ѧһģ�Ծ� ���ͣ������
����С������10�֣�
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.
���Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad��.��ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=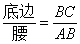 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
���������Խǵ����Զ��壬���������⣺
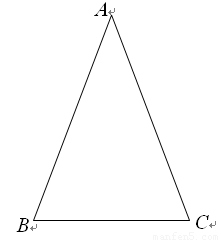
��1��sad  ��ֵΪ�� ��A.
��ֵΪ�� ��A. 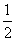 B.
1 C.
B.
1 C. 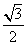 D.
2
D.
2
��2������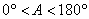 ����A������ֵsad A��ȡֵ��Χ��
.
����A������ֵsad A��ȡֵ��Χ��
.
��3����֪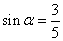 ������
������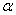 Ϊ��ǣ�����sad
Ϊ��ǣ�����sad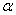 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com