练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如图，已知正方形ABCD的边长为2，将正方形ABCD沿直线EF折叠，则图中阴影部分的周长为8．

    分析 根据翻折的性质以及拆分三角形，即可得出阴影部分的周长等于正方形ABCD的周长，再根据正方形的周长公式即可得出结论．

    解答 解：根据翻折的性质可知：图形阴影部分的周长等于正方形ABCD的周长，
    C阴影=C正方形ABCD=4×2=8．
    故答案为：8．

    点评 本题考查了翻折变换以及正方形的性质，解题的关键是找出阴影部分的周长等于正方形ABCD的周长．本题属于基础题，难度不大，解决该题型题目时，根据翻折的性质找出相等的边角关系是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．如图，△ABC绕点A逆时针旋转到△AB1C1，∠CAC1=75°，AB1∥BC1，则旋转角为（　　）
    A．120°B．110°C．100°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

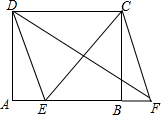    15．在矩形ABCD中，AD=3，AB=4，点E在线段AB上，将AE平移至BF．
    （1）是否存在点E，使得四边形DEFC为菱形？若存在，求出AE长，不存在，说明理由．
    （2）直接写出DF、CE、AE之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，已知三角形ABC中，∠A=56°，∠ABC=90°，AB=8cm，BC=12cm，现将三角形ABC沿直线CB向左平移xcm（x＜12，且x是正数），得到新的三角形DEF，DF交AB与点G．
    （1）求∠BGF的度数；
    （2）若x=3，BG=6cm，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列各分式不能再化简的是（　　）
    A．$\frac{2}{x-2}$B．$\frac{m-1}{1-m}$C．$\frac{xy-y}{2xy}$D．$\frac{a+b}{{a}^{2}-{b}^{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称．
    （1）画出对称中心E，并写出点E的坐标（-3，-1）；
    （2）画出△A1B1C1绕点O逆时针旋转90°后的△A2B2C2；
    （3）画出与△A1B1C1关于点O成中心对称的△A3B3C3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，平面直角坐标系中，把点A（-3，-1）向右平移5个单位得到B点，再把B点向上平移6个单位得到C点．
    （1）点O为坐标系原点．连接OA、OC、AC，求三角形AOC的面积S；
    （2）设直线AC与y轴交于点M，现有一动点P从原点O出发，沿y轴的正方向向上运动，速度为每秒0.2个单位长度，运动时间为t秒，求点P在线段OM上和在线段OM外运动时，t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，郑梦将一个三角形纸板ABC沿直线BC向右平移得到新的三角形DEF，使点E与点C重合，经测量得到∠BAC=40°，EF=4cm，三角形ABC的周长为16cm，连接AD，则下列说法中不正确的是（　　）
    A．∠EDF=45°B．AB∥CD
    C．四边形ABFD的周长为20cmD．AD∥BF

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，每个小正方形的边长为1，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．根据下列条件，利用网格点和三角板画图：

    （1）补全△A′B′C′
    （2）画出AB边上的中线CD；
    （3）画出BC边上的高线AE；        
    （4）△A′B′C′的面积为8．

    查看答案和解析>>

    同步练习册答案