
����Ŀ���Ķ�����
��̽���뷢�֣�
��һ����ѧ̽����У���ѧ��ȤС��ͨ��̽�����ֿ���ͨ�����������IJ�������ʾ�������������ľ�������ͼ1�������߶εij��ȿɱ�ʾΪ��AB=4-2=2��CB=4-(-2)=6��DC=-2-(-4)=2�������ۣ����������������ʾ����Ϊ�ֱ�a��b(b��a)�������������ľ���Ϊb-a(�����ýϴ������ȥ��С����)

�����������ã�
(1)��ͼ2��������E��F�����ʾ�����ֱ�Ϊ-2��-5���Լ��㣺EF=______��AF=______��
(2)�������Ϸֱ���������M��N��H����������M��ʾ����Ϊ-18����N��ʾ����Ϊ2018����֪��HΪ�߶�MN�е㣬����H��ʾ����m���������m��ֵ��
����չ�����죩
(3)��ͼ3����A��ʾ��x����B��ʾ-1����C��ʾ3x+8����AB=![]() BC�����A�͵�C�ֱ��ʾʲô����
BC�����A�͵�C�ֱ��ʾʲô����
(4)��(3)�����£���ͼ3���������Ƿ�������������ĵ�D��ʹDA+DC=3DB�������ڣ���ֱ��д����D��ʾ�������������ڣ���˵�����ɣ�
���𰸡�(1)3�� 7��(2)m=1000��(3)��A��ʾ��-2����C��ʾ������2��(4)��D����ʾ������-3��-![]() .
.
��������
��1�����õó��Ľ���ֱ�Ӽ��㼴�ɣ�
��2�����öԳƵ������з��̽�ɣ�
��3������ͼ��ʾ����������BC=4AB������������ô𰸣�
��4�������D��ʾ���������������г�����̽�ֵó��𰸼��ɣ�
(1)EF=-2-(-5)=3��FA=2-(-5)=7��
(2)m-(-18)=2018-m��
���m=1000��
(3)![]()
��ã�x=-2��
3x+8=2��
��A��ʾ��-2����C��ʾ������2��
(4)���ڣ����D��ʾ����Ϊd����������ã�-2-d+2-d=3(-1-d)���d=-3��
��d+2+2-d=3(d+1)�����![]() �ʵ�D����ʾ������-3��
�ʵ�D����ʾ������-3��![]() ��
��
�ʵ�D����ʾ������-3��![]() ��
��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ��11�µ����һ���������Ǹж��ڣ�С�������˳����꼶����ͬѧ�ڸж��ڵ��콫�Ժ��ַ�ʽ�����л�������Լ����ˣ�������������Ϊ�������ࣺA�ੁ��������л��B�ੁ����绰��C�ੁ��������Ϣ���ţ�D�ੁ��д���ţ��������������Ƴ���ͼ������������ͳ��ͼ������ͳ��ͼ��
�������ͼ���ṩ����Ϣ������и��⣺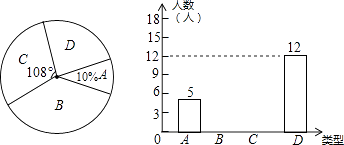
��1����ȫ����ͳ��ͼ��
��2����A���ͬѧ�У���3������ͬһ�༶��������1��ѧ�����֣�����������3������������λͬѧ���ָж���������Σ���������״ͼ����������������˶�û��ѧ�����ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ��ڽ���ƽ��ֱ������ϵ���SABC�Ķ����ڸ���ϡ� ��A��1��-4����B��5��-4����C��4��-1��
��1�������SABC��
��1������SABC �������![]()
��1�������SABC����ƽ��2����λ���ȣ�������ƽ��4����λ���ȵõ��S![]()
![]() B
B![]() C
C![]() ����ͼ�л����S
����ͼ�л����S![]()
![]() B
B![]() C
C![]() �����B
����д��B![]() �����ꡣ
�����ꡣ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��Ϊ���̻��������ƻ������ι���A��B���ֻ��ݣ���һ�ηֱ�A��B���ֻ���30�ú�15�ã�������675Ԫ���ڶ��ηֱ�A��B���ֻ���12�ú�5�ã�������265Ԫ�����ι�����A��B���ֻ��ݼ۸���ֱ���ͬ����
��1��A��B���ֻ���ÿ�õļ۸�ֱ��Ƕ���Ԫ��
��2��������A��B���ֻ��ݹ�31�ã���B�ֻ��ݵ���������A�ֻ��ݵ�������2�����������һ�ַ�����ʡ�ķ�����������÷���������ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����·�����׳���A�ص�B�����ҳ���B�ص�A�������ȳ�����ͼ�е����߶α�ʾ�ס�������֮��ľ���y��ǧ�ף�����ʻʱ��x��Сʱ���ĺ�����ϵ��ͼ��������˵��������ǣ�������
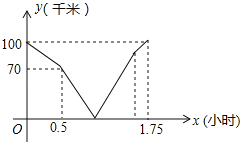
A. ���ȳ�����ʱ��Ϊ0.5Сʱ B. ���ٶ���80ǧ��/Сʱ
C. �׳���0.5Сʱ���������� D. ��B�ر��ҵ�A����![]() Сʱ
Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������ɸ��ᡢ������Ϊ�����ĵ㣬��˳��ͼ�С������������У���ԭ�㿪ʼ����Ϊ��0��0������1��0������1��1������0��1������0��2������1��2������2��2������2��1������2��0����3��0�������˹��ɵ�200�����������_____��
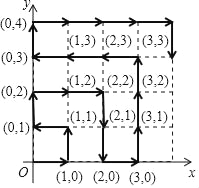
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
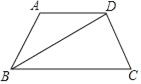
����Ŀ����ͼ���ı���ABCD�У�AD��BC����A��120�㣬BDƽ�֡�ABC��
��1����BD��CD�����C�Ķ�����
��2������AP��ABλ�ÿ�ʼ����ÿ��10����ٶ��Ƶ�A��ʱ����ת��6���AP��BD�к���λ�ù�ϵ����˵�����ɣ�
��3���ڣ�2���������£�AP��תһȦ�ص�AB��ʱֹͣ�˶���������AP��ֱ��BD�ཻ���ɵĽ��н�С�Ľ�Ϊx�㣬��10��x��20������תʱ��t����λ���룩��ȡֵ��Χ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3��a��0������A��3��0����B��4��1�����㣬����y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2����ͼ��1��������������x�����һ������ΪD���������ߵĶԳ�������һ��H��ʹ��CDH���ܳ���С�����H������겢�����С�ܳ�ֵ��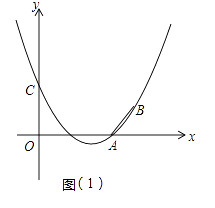
��3����ͼ��2��������AC��EΪ�߶�AC������һ�㣨����A��C�غϣ�������A��E��O�����Բ��ֱ��AB�ڵ�F������OEF�����ȡ����Сֵʱ�����������Сֵ��E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ������5������ɫ�⣬��������ͬ��С��������3���Ǻ���2��������ÿ����һ����Ȼ��Ż�ȥ����2�Σ���������һ��ȡ������ĸ����� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com