
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 1 |
| 2 |
| 1 |
| x2-2x+1 |
| x2-2 |
| x-1 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
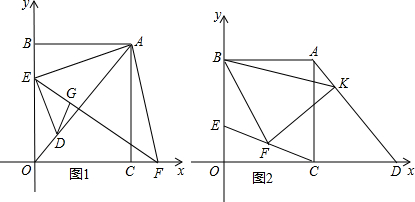
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
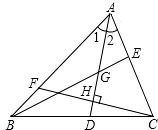 如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线,其中判断正确的有
如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线,其中判断正确的有查看答案和解析>>
科目:初中数学 来源: 题型:
| 项目 | 开幕式 | 篮球 | 足球 | 乒乓球 | 排球 | 跳水 | 体操 | 田径 | 射击 | 举重 | 羽毛球 | 闭幕式 |
| 价格 | 200 | 50 | 40 | 50 | 50 | 60 | 100 | 50 | 30 | 30 | 50 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com