Question

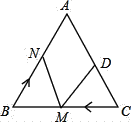
【题目】如图，在等边中，厘米，厘米.如果点以厘米/秒的速度运动，如果点在线段上由点向点运动，点在线段上由点向点运动.它们同时出发，若点的运动速度与点的运动速度相等.

(1)经过秒后，和是否全等？请说明理由.

(2)当两点的运动时间为多少时，是一个直角三角形？

Answer 1

【答案】（1）△BMN≌△CDM．理由见解析；

（2）当t=秒或t=秒时，△BMN是直角三角形.

【解析】

（1）根据题意得CM=BN=6cm，所以BM=4cm=CD．又∠B=∠C=60°，根据“SAS”可证明△BMN≌△CDM；
(2)设运动时间为t秒，分别表示出CM和BN．分①∠NMB=90°；②∠BNM=90°两种情况，运用直角三角形的性质求解.

解：（1）△BMN≌△CDM．理由如下：
∵VN=VM=3厘米/秒，且t=2秒，
∴CM=2×3=6（cm）
BN=2×3=6（cm）
BM=BC-CM=10-6=4（cm）
∴BN=CM
∵CD=4（cm）
∴BM=CD
∵∠B=∠C=60°，
∴△BMN≌△CDM．（SAS）
（2）设运动时间为t秒，△BMN是直角三角形.

有两种情况：
①当∠NMB=90°时，
∵∠B=60°，
∴∠BNM=90°-∠B=90°-60°=30°．
∴BN=2BM，
∴3t=2×（10-3t）
∴t=（秒）；
②当∠BNM=90°时，
∵∠B=60°，
∴∠BMN=90°-∠B=90°-60°=30°．
∴BM=2BN，
∴10-3t=2×3t
∴t=（秒）
∴当t=秒或t=秒时，△BMN是直角三角形.