
 .
.
 绕点M顺时针旋转
绕点M顺时针旋转 (30
(30 到
到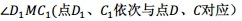 ,射线
,射线 交直线CB于点F,设DE=m,BF=n,求m与n的函数关系式.
交直线CB于点F,设DE=m,BF=n,求m与n的函数关系式.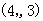 ,∴直线CB的解析式为:
,∴直线CB的解析式为: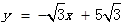 …2分
…2分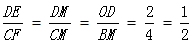 ∴CF=2DE.
∴CF=2DE.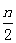 (0<n<4); ……………8分
(0<n<4); ……………8分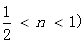 ……………10分
……………10分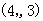 ,从而求得直线CB的解析式
,从而求得直线CB的解析式

科目:初中数学 来源:不详 题型:单选题

| A.(4.8,6.4) | B.(4,6) | C.(5.4,5.8) | D.(5,6) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:①乙往返行程中的平均速度相同;②乙从学校出发45分钟后追上甲;③乙从
地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:①乙往返行程中的平均速度相同;②乙从学校出发45分钟后追上甲;③乙从 地返回到学校用时1小时18分钟;④甲、乙返回时在下坡路段相遇.其中正确的结论有 ▲ (填“序号”)
地返回到学校用时1小时18分钟;④甲、乙返回时在下坡路段相遇.其中正确的结论有 ▲ (填“序号”)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com