练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y=x2+bx+c的图象经过点A（－1，12），B（2，－3）.

    （1）求这个二次函数的解析式；

    （2）求这个图象的顶点坐标及与x轴的交点坐标.

    【答案】（1）y=x2-6x+5；（2）（1，0） （5，0）

    【解析】

    （1）根据待定系数法,把点A（-1,12）,B（2,-3）的坐标代入y=x2+bx+c得:

    ,解方程组可得:,因此二次函数关系式是:y=x2-6x+5,

    （2）根据二次函数顶点坐标公式代入即可求出顶点（3,-4）,根据二次函数与一元二次方程的关系,令x2-6x+5=0,解得x1=1,x2=5, 因此求得二次函数与x轴的交点坐标为（1,0）, （5,0）.

    （1）把点A（-1,12）,B（2,-3）的坐标代入y=x2+bx+c得:

    ,解得:,

    ∴y=x2-6x+5,

    （2）顶点（3,-4）,

    令x2-6x+5=0,解得x1=1,x2=5,

    ∴与x轴的交点坐标为（1,0）, （5,0）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，某住宅小区在施工过程中留下了一块空地，已知AD=8米，CD=6米，∠ADC=90°，AB=26米，BC=24米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问用该草坪铺满这块空地共需花费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小亮将笔记本电脑水平放置在桌子上，显示屏OA与底板OB所在水平线的夹角为120°时，感觉最舒适（如图1），侧面示意图为图2；使用时为了散热，她在底板下面垫入散热架BCO＇后，电脑转到B O′A′位置（如图3）,侧面示意图为图4.已知OA=OB=28cm，O′C⊥OB于点C，O′C=14cm.

    （参考数据：，，）

    （1）求∠CBO＇的度数.

    （2）显示屏的顶部A＇比原来升高了多少cm？（结果精确到0.1cm）

    （3）如图4，垫入散热架后，要使显示屏O′A′与水平线的夹角仍保持120°，则显示屏O′A′应绕点O＇按顺时针方向旋转多少度？（不写过程，只写结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了迎接“六一”儿童节．某儿童运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：

    运动鞋

    价格

    甲

    乙

    进价（元/双）

    m

    m﹣20

    售价（元/双）

    240

    160

    已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．

    （1）求m的值；

    （2）要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？该专卖店要获得最大利润应如何进货？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y＝ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），顶点为D．

    （1）求抛物线的解析式；

    （2）设点M（1，m），当MB+MD的值最小时，求m的值；

    （3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)观察猜想

    如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°，AD=AE,则BC、BD、CE之间的数量关系为

    (2)问题解决

    如图②,在Rt△ABC中,∠ABC=90°，CB=8，AB=4，以AC为直角边向外作等腰Rt△DAC连接BD,求BD的长。

    (3)拓展延伸

    如图③,在四边形ABCD中,∠ABC=∠ADC=90°，CB=8.AB=4，DC=DA，则BD=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】七（1）班同学为了解2018年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，请解答以下问题：

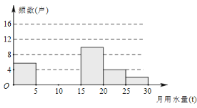
    （1）求，的值．并把频数直方图补充完整；

    （2）求该小区用水量不超过的家庭占被调在家庭总数的百分比；

    （3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水是超过的家庭大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题满分12分）在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．

    （1）小明发现，请你帮他说明理由．

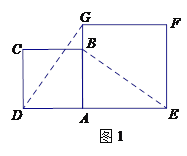
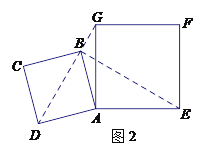
    （2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．

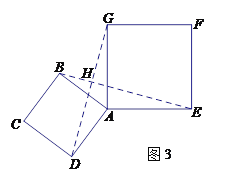
    （3）如图3，若小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△与△面积之和的最大值，并简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC≌△A′B′C，∠ACB=90°，∠B=50°，点B′在线段AB上，AC，A′B′交于点O，则∠COA′的度数是（ ）

    A.50°B.60°

    C.45°D.80°

    查看答案和解析>>

    同步练习册答案