
分析 (1)只要证明△>0即可;
(2)由一元二次方程根与系数的关系可知:
解答 解:(1)令y=0得:x2-(m-2)x-$\frac{{m}^{2}}{4}$=0,
△=$[-(m-2)]^{2}-4×(-\frac{{m}^{2}}{4})$
=(m-2)2+m2
=(m-1)2+2≥2,
∴无论m取什么实数,抛物线总与x轴有两个不同交点;
(2)令y=0得:x2-(m-2)x-$\frac{{m}^{2}}{4}$=0,
由一元二次方程根与系数的关系可知:x1+x2=m-2①,${x}_{1}{x}_{2}=-\frac{{m}^{2}}{4}$②.
由①平方得:${x}_{1}^{2}+{x}_{2}^{2}+2{x}_{1}{x}_{2}$=(m-2)2,
∴${x}_{1}^{2}+{x}_{2}^{2}$=$(m-2)^{2}+\frac{{m}^{2}}{2}$③.
∵|x2|=|x1|+2,
∴|x2|-|x1|=2.
∴${x}_{1}^{2}+{x}_{2}^{2}-2|{x}_{1}{x}_{2}|=4$
∴$(m-2)^{2}+\frac{{m}^{2}}{2}-2×|-\frac{{m}^{2}}{4}|=4$.
整理得:(m-2)2=4.
∴m=4或m=0.
点评 本题主要考查的是二次函数与x轴交点的问题,将函数问题转化为方程问题是解题的关键.


科目:初中数学 来源: 题型:选择题
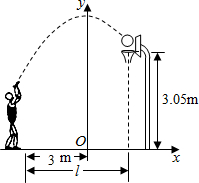 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
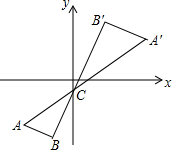 如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C. | -$\frac{b}{a}$ | D. | $\frac{c}{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com