
����Ŀ��ij�����û�������ij�ֻ��磬�������鷢��ÿ���ӯ����ÿ�����������һ���Ĺ�ϵ��ÿ��ֲ��3��ʱ��ƽ������ӯ��3Ԫ����ͬ����������������ÿ������1�꣬ƽ������ӯ���ͼ���0.5Ԫ��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ�����ꣿ С���Ľⷨ���£�
�⣺��ÿ�軨������x�꣬��ÿ�軨���У�x+3���꣬ƽ������ӯ��Ϊ��3��0.5x��Ԫ��
������ã�x+3����3��0.5x��=10��
���������ã�x2��3x+2=0
��������̣��ã�x1=1��x2=2��
��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ��4���5�꣮
��1�������漰����Ҫ������ÿ�軨��������ƽ������ӯ����ÿ�軨���ӯ���ȣ���д��������ͬ�ĵ�����ϵ�� ��
��2������һ����С������ͬ�ķ�������������⣮
���𰸡�
��1��ƽ������ӯ����ÿ������=ÿ��ӯ����ƽ������ӯ��=3��0.5��ÿ�����ӵ�����
��2���⣺�ⷨ1���б�����
ÿ��ֲ������ | ƽ������ӯ����Ԫ�� | ÿ��ӯ����Ԫ�� |
3 | 3 | 9 |
4 | 2.5 | 10 |
5 | 2 | 10 |
6 | 1.5 | 9 |
7 | 1 | 7 |
��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ��4���5�ꣻ
�ⷨ2��ͼ��
��ͼ�������ʾƽ������ӯ���������ʾ����������Ӧ�����������ʾÿ��ӯ����
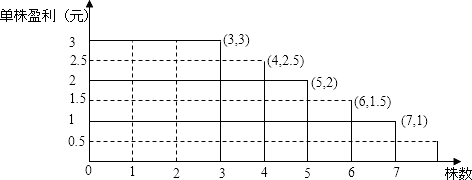
��ͼ���֪��ÿ��ֲ��4���5��ʱ����Ӧ�������������10
��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ��4���5�꣮
�ⷨ3����������
�⣺��ÿ�軨������x��ÿ���ӯ��ΪyԪ����������ÿɵã�y=��x+3����3��0.5x����
��y=10ʱ����x+3����3��0.5x��=10��
��������̵ã�x1=1��x2=2��
��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ��4��5�ꣻ
�ⷨ4���з�ʽ���̣�
�⣺��ÿ�軨������x��ʱ��ÿ��ӯ��10Ԫ���������⣬�ã�
![]() ��
��
��������̵ã�x1=1��x2=2��
�����飬x1=1��x2=2�������з��̵Ľ⣬
��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ��4��5��
���������⣺��1��ƽ������ӯ����ÿ������=ÿ��ӯ���� ƽ������ӯ��=3��0.5��ÿ�����ӵ���������1�����������д��ƽ������ӯ��������=ÿ��ӯ����ƽ������ӯ��=3��0.5��ÿ�����ӵ���������2�����˷��̷��������б�����ͼ�ͺ�������ͬѧ�ǿ�ѡ���Լ�ϲ���ķ���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8����2014��12��28���������������Ǽ���·��ʽ��ͨ������̨�������ĸ�����̱��տ����������81ǧ��������ʱ�������9Сʱ����֪��̨���������տ��г������1026ǧ��������ƽ��ʱ�����տ�ƽ��ʱ�ٵ�2��5����
��1��������г���ƽ��ʱ�٣�
��2��ij������ʦҪȥ������̨��Լ630ǧ��ij�вμ�14:00�ٿ��Ļ������������
����8:40����̨�����ǵĸ���Ʊ�����ҴӸ��л�վ������ص������Ҫ1��5Сʱ�������ڸ����г��㵽�������������ڿ���֮ǰ�ϵ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǵ���Ľ��ڣ�������Դһֱ�������̽��������֮һ��ȫ�����������126������̽������Ϊ�о���������������������ʶ��������ʶ̫��ϵ���ݻ����ص㣬��ʶ������Ȼϵͳ��̫����Ȼ����֮��Ĺ�ϵ�������Ѿ���ʶ������������棬�������ⴹֱ����ĵط��¶ȸߴ�127�棬ҹ���¶ȿɽ�����183�森���������183��������������ȷ���ǣ�������

A. ��183��һ������
B. ��183��ʾ�ں�ƽ������183��
C. ��183�������ϵ�λ����ԭ������
D. ��183��һ���ȩ�100С����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в�������2006��5�������й�ý�����ʵ�������йز��Ž������ڰ�ȫ������ȵ��飬�����ǣ���ȫ���ڲ��õȾ��������ȡ32��С������960����ÿ����һ������16���겢���������������ˣ�ͬʱ���Ա�ǰһ��ĵ��������õ�ͳ��ͼ���£� 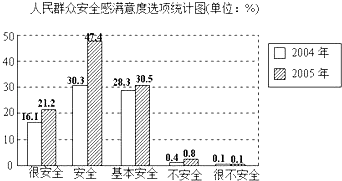
д��2005�����ڰ�ȫ������ȵ�����ѡ��������ͳ��ͼ����һ�����ԵĴ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㹻��ij����κ������ο�Ƭ������ͼ�� 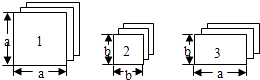
��1�����ѡȡ1�š�2�š�3�ſ�Ƭ�ֱ�Ϊ1�š�2�š�3�ţ���ƴ��һ�������Σ����ص���϶�����뻭����������εIJ�ͼ��������ƴͼǰ�����֮��Ĺ�ϵ˵����������εĴ������壮 
��������εĴ��������� ��
��2��С���������Ʒ������Ͷ���ʽ�˷���a+3b����2a+b��=2a2+7ab+3b2 �� ��ô����2�ſ�Ƭ�ţ�3�ſ�Ƭ�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD=8����A=60�㣬��ADC=150�����ı���ABCD���ܳ�Ϊ32��
��1�����BDC�Ķ�����
��2���ı���ABCD�������
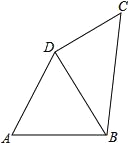
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����DΪ����ֱ����ABC��һ�㣬��ACB=90�㣬��CAD=��CBD=15�㣬EΪAD�ӳ�����һ�㣬��CE=CA���������½��ۣ���DEƽ����BDC�� �ڡ�BCE�ǵȱ������Σ��ۡ�AEB=45�㣻��DE=AD+CD����ȷ�Ľ�����_____����������ţ�
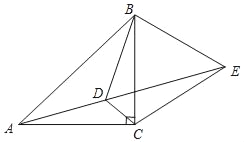
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��CΪ�߶�AE��һ���㣨�����A��E�غϣ�����AEͬ��ֱ�����������ABC����������CDE��AD��BE���ڵ�O��AD��BC���ڵ�P��BE��CD���ڵ�Q������PQ.����������ۣ���AD=BE����PQ��AE����AP=BQ����DE=DP���ݡ�AOB=60��. ������Ľ�����( )
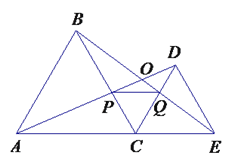
A. �٢ۢܢ� B. �٢ڢܢ�
C. �٢ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ������˿�������ת����ת�̣���ͼ��ת�̱����ȷ�Ϊ20�ݣ������涨���˿�ÿ����200Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���200Ԫ��100Ԫ��50Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��תת�̣���ô����ֱ�ӻ�ù���ȯ30Ԫ��
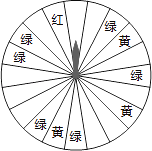
��1����ת��һ��ת�̻�ù���ȯ�ĸ��ʣ�
��2��תת�̺�ֱ�ӻ�ù���ȯ������Ϊ���ַ�ʽ�Թ˿����㣿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com