
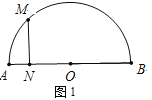
【题目】如图1,半圆O的半径![]() =5cm,点N是半径AO上的一个动点(不与A、O重合),沿AO方向以1cm/s的速度向O点运动,过点N作MN⊥AB,交半圆O于点M,设运动时间为t s.
=5cm,点N是半径AO上的一个动点(不与A、O重合),沿AO方向以1cm/s的速度向O点运动,过点N作MN⊥AB,交半圆O于点M,设运动时间为t s.
(1)求当t等于多少时,MN=3cm?
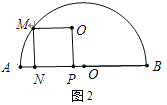
(2)如图2,以MN为边在半圆O内部作正方形MNPQ,使得点P落在AB上,点Q落在半圆内(或半圆上),设正方形MNPQ的面积为S.求S与t之间的函数关系式与自变量t的取值范围.
【答案】(1)当t等于1时,MN=3cm;
(2)S与t之间的函数关系式为![]() ,自变量t的取值范围是:
,自变量t的取值范围是: ![]() .
.
【解析】27. (1)

连接OM
∵MN⊥OA
∴ 在Rt△MNO中,OM=5,MN=3
∴ON=![]() ………………………2分
………………………2分
∴AN=AO-NO=1cm ………………………3分
∴t=1………………………………4分
(2)连接OM
∵AN=t
∴NO=5-t ……………………………5分
∴由勾股定理可得:

MN 2=OM 2-ON 2=![]() ……7分∴
……7分∴![]() …8分
…8分
当Q落在半圆上时,如图所示,连接OM、OQ
则OM=OQ
∴Rt△MNO≌Rt△QPO (HL)
∴ON=OP
∵AN=t∴NO=5-t
∴MN=NP=2(5-t)=10-2t……………………………9分
由勾股定理可得:MN2+ON2=OM2 即![]()
解得:t=![]() (舍去)或
(舍去)或![]() …………………10分
…………………10分
∴t的取值范围是: ![]() …………………11分
…………………11分


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】在□ABCD中,对角线AC,BD相交于O点,AC=10,BD=8,则AD长的取值范围是 ( )
A. AD>1 B. AD<9 C. 1<AD<9 D. AD>10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°③BE+DF=EF;④CE= ![]() ,其中正确的结论的个数为( )
,其中正确的结论的个数为( )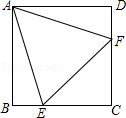
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”1 176万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com