
【题目】如图,已知直线y=![]() x+2与x轴、y轴分别交于点B,C,抛物线y=
x+2与x轴、y轴分别交于点B,C,抛物线y=![]() x2+bx+c过点B、C,且与x轴交于另一个点A.
x2+bx+c过点B、C,且与x轴交于另一个点A.
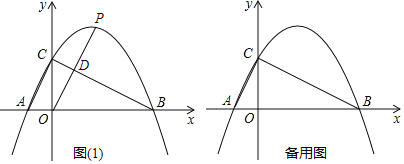
(1)求该抛物线的表达式;
(2)若点P是x轴上方抛物线上一点,连接OP.
①若OP与线段BC交于点D,则当D为OP中点时,求出点P坐标.
②在抛物线上是否存在点P,使得∠POC=∠ACO若存在,求出点P坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①点P坐标为(2,3);②存在点P(
x+2;(2)①点P坐标为(2,3);②存在点P(![]() ,
,![]() ﹣1)或(
﹣1)或(![]() ,
,![]() ﹣7)使得∠POC=∠ACO
﹣7)使得∠POC=∠ACO
【解析】
(1)![]() 与x轴、y轴分别交于点B(4,0)、C(0,2),由题意可得
与x轴、y轴分别交于点B(4,0)、C(0,2),由题意可得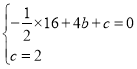 即可求解;
即可求解;
(2)①过点P作PE∥OC,交BC于点E.根据题意得出△OCD≌△PED,从而得出PE=OC=2,再根据 ![]() 即可求解;
即可求解;
②当点P在y轴右侧,PO∥AC时,∠POC=∠ACO.抛物线与x轴交于A,B两点,点A在点B左侧,则点A坐标为(-1,0).则直线AC的解析式为y=2x+2.直线OP的解析式为y=2x,即可求解;当点P在y轴右侧,设OP与直线AC交于点G,当CG=OG时,∠POC=∠ACO,根据等腰三角形三线合一,则CF=OF=1,可得:点G坐标为![]() 即可求解.
即可求解.
(1)∵y=﹣![]() x+2与x轴、y轴分别交于点B(4,0)、C(0,2).
x+2与x轴、y轴分别交于点B(4,0)、C(0,2).
由题意可得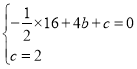 ,解得:
,解得:![]() ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)①如图,过点P作PE∥OC,交BC于点E.
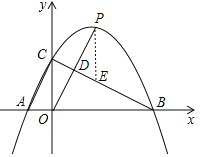
∵点D为OP的中点,
∴△OCD≌△PED(AAS),
∴PE=OC=2,
设点P坐标为(m,﹣![]() m2+
m2+![]() m+2),点E坐标为(m,﹣
m+2),点E坐标为(m,﹣![]() m+2),
m+2),
则PE=(﹣![]() m2+
m2+![]() m+2)﹣(﹣
m+2)﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+2m=2,
m2+2m=2,
解得m1=m2=2.
∴点P坐标为(2,3);
②存在点P,使得∠POC=∠ACO.
理由:分两种情况讨论.
如上图,当点P在y轴右侧,
PO∥AC时,∠POC=∠ACO.
∵抛物线与x轴交于A,B两点,点A在点B左侧,
∴点A坐标为(﹣1,0).
∴直线AC的解析式为y=2x+2.
∴直线OP的解析式为y=2x,
解方程组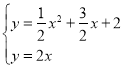 ,解得:x=
,解得:x=![]() (舍去负值)
(舍去负值)
∴点P坐标为(![]() ,
,![]() ﹣1).
﹣1).
如图,当点P在y轴右侧,
设OP与直线AC交于点G,当CG=OG时∠POC=∠ACO,
过点G作GF⊥OC,垂足为F.
根据等腰三角形三线合一,则CF=OF=1.
∴可得点G坐标为(﹣![]() ,1)
,1)
∴直线OG的解析式为y=﹣2x;
把y=﹣2x代入抛物线表达式并解得x=![]() (不合题意值已舍去).
(不合题意值已舍去).
∴点P坐标为(![]() ,
,![]() ﹣7).
﹣7).
综上所述,存在点P(![]() ,
,![]() ﹣1)或(
﹣1)或(![]() ,
,![]() ﹣7)使得∠POC=∠ACO.
﹣7)使得∠POC=∠ACO.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
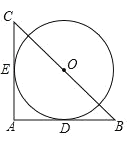
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
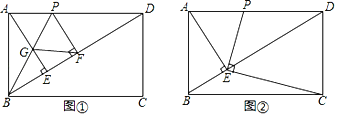
(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;
(2)若PE⊥EC,如图②,求证:AEAB=DEAP;
(3)在(2)的条件下,若AB=1,BC=2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元一世纪左右.在其“勾股”章中有这样一个问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD.EG=15里,HG经过点A,则FH等于多少里?请你根据上述题意,求出FH的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
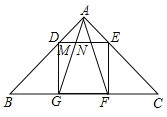
【题目】如图,在△ABC中,AB=AC=3![]() ,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于点M和点N,则线段MN的长为_____.
,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于点M和点N,则线段MN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 与一次函数y2=ax+b的图象交于点A(﹣2,5)和点B(n,l).
与一次函数y2=ax+b的图象交于点A(﹣2,5)和点B(n,l).
(1)求反比例函数和一次函数的表达式;
(2)请结合图象直接写出当y1≥y2时自变量x的取值范围;
(3)点P是y轴上的一个动点,若S△APB=8,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
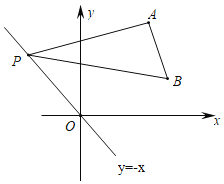
【题目】如图,在平面直角坐标系中,点A的坐标为(2![]() ,2
,2![]() ),点P在直线y=﹣x上运动,∠PAB=90°,∠APB=30°,在点P运动的过程中OB的最小值为( )
),点P在直线y=﹣x上运动,∠PAB=90°,∠APB=30°,在点P运动的过程中OB的最小值为( )
A.3.5B.2C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com