
(2005 烟台)(1)如图a所示,直线MN与⊙O相交,且与⊙O的直径AB垂直,垂足为P,过点P的直线与⊙O交于C、D两点,直线AC交MN于点E,直线AD交MN于点F.

a)
求证:(1)PC·PD=PE·PF;
(2)如图b所示,若直线MN与⊙O相离,(1)中的其余条件不变,那么(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由;

b)
(3)在图c中,直线MN与⊙O相离,且与⊙O的直径AB垂直,垂足为P.①请按要求画出图形:画⊙O的割线PCD(PC<PD,直线BC与MN交于E,直线BD与MN交于F.

c)
②能否得到(1)中的结论?请说明理由.
|
解 (1)证明:如图所示,连接BD
∵AB是⊙O直径, ∴∠ ADB=90°.∴∠ ADC+∠BDC=90°.∵MN⊥AB,∴∠ AEP+∠BAC=90°.∵∠ BAC=∠BDC,∴∠ADC=∠AEP.∵∠ DPF=∠EPC,∴△PDF∽△PEC.∴ 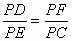 . .
∴ PC·PD=PE·PF.(2) 结论仍然成立.证明:如图所示,连接 BD.
∵ AB是⊙O直径,∴∠ADB=90°.∴∠ ABD+∠BAD=90°.∵∠ ACD=∠PCE,∠ABD=∠ACD,∴∠ PCE+∠BAD=90°.∵ MN⊥AB,∴∠PFA+∠BAD=90°.∴∠ PCE=∠PFA.∴∠EPC=∠FPD,∴△ PCE∽△PFD.∴ 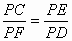 . .
∴ PC·PD=PE·PF.(3) 画图(图),结论仍然成立.证明:如图
连接AC ∵ AB为⊙O的直径,∴∠ACB=90°∵AP⊥MN,∴∠BPE=90°.∵∠ ABC=∠EBP,∴∠A=∠PEB.又∵∠ D=∠A,∴∠D=∠PEB.又∠DPE公用,∴△ DPF∽△EPC.∴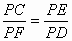 . .
∴ PC∶PD=PE∶PF. |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:013
(2005 烟台)△ABC中,∠ACB=90°,∠B=30°,AC=1,过点C作 于
于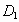 ,过点
,过点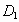 作
作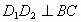 于
于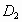 ,过点
,过点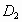 作
作 于
于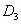 ,这样继续下去,线段
,这样继续下去,线段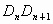 (n为正整数)等于
(n为正整数)等于
[ ]
|
A. |
B. |
C. |
D. |
查看答案和解析>>
科目:初中数学 来源: 题型:044
(2005 烟台)先阅读下面材料,然后解答问题.
王老师在黑板上出了这样一道习题:设方程 的两个实数根是
的两个实数根是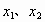 ,请你选取一个适当的k值,求
,请你选取一个适当的k值,求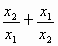 的值.
的值.
小明同学取k=4,他作了如下解答:
取k=4,则方程是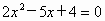 .
.
由根与系数关系,得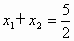 ,
,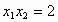 .
.
∴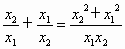
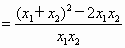
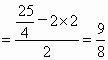 .
.
即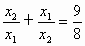 .
.
问题(1):请你对小明解答的正误作出判断,并说明理由.
问题(2):请你另取一个适当的正整数k,其他条件不变,不解方程,改求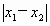 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:044
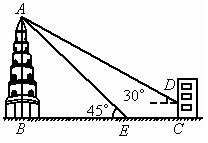
(2005 烟台)某风景区内有一古塔AB,在塔的北面有一建筑物,冬至日的正午光线与水平面的夹角是30°,此时塔在建筑物的墙上留下了高3m的影子CD;而在春分日正午光线与地面的夹角是45°,此时塔尖A在地面上的影子E与墙角C有15m的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号,见图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com