



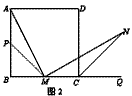
| (1)①填空:当∠AMN =90°时,AM=MN; ②证明:取的AB中点P,连结PM ∵四边形ABCD是正方形 ∴∠PAM +∠AMB =90° ∵∠AMN =90° ∴∠CMN+∠AMB =90° ∴∠PAM = CMN ∵点M是边BC的中点 点P是边AB的中点 AB=BC ∴AP=MC BP=BM ∵∠B =90° ∴△BPM是等腰直角三角形 ∴∠BPM =45° ∴∠APM =135° ∵∠DCB =90° ∴∠DCQ =90° ∴∠NCQ =45° ∴∠MCN =135° ∴∠APM =∠MCN ∴△APM ≌△MCQ ∴AM=MN. |
 |
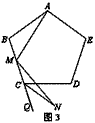
| (2)正五边形ABCDE中点M是边BC的中点,CN是正五 边形ABCDE的外角∠DCQ的平分线,当∠AMN =108°. 求证:AM=MN. |
 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
 +b+c的正方形来研究.
+b+c的正方形来研究.| a2+b2 |
| b2+c 2 |
| a2+c2 |
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
| x2+4 |
| y2+9 |
| a2+b2 |
| 4a2+b2 |
| a2+4b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
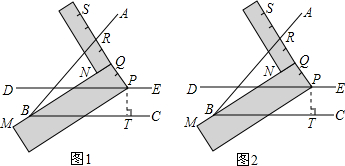 (1)阅读理解:
(1)阅读理解: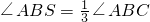 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出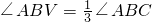 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com