

分析 (1)过A作AF⊥BC,交CB的延长线于F,求出四边形AFCE是矩形,根据矩形的性质得出∠FAE=90°,求出∠DAE=∠BAF=90°-∠BAE,根据AAS得出△AFB≌△AED,根据全等得出AE=AF=10,S△AFB=S△AED,求出S正方形AFCE=100,求出S四边形ABCD=S正方形AFCE,代入求出即可;
(2)过A作AF⊥CD,交CD的延长线于F,求出∠BAE=∠FAD,根据AAS推出△AEB≌△AFD,根据全等得出AE=AF=19,BE=DF,设BE=DF=x,由勾股定理得出AC2=AE2+CE2=AF2+CF2,推出10-x=6+x,求出x,求出S正方形AFCE=152和S四边形ABCD=S正方形AFCE,代入求出即可.
解答 解:(1)如图1,过A作AF⊥BC,交CB的延长线于F, ∵AE⊥CD,∠C=90°
∵AE⊥CD,∠C=90°
∴∠AED=∠F=∠C=90°,
∴四边形AFCE是矩形,
∴∠FAE=90°,
∵∠DAB=90°,
∴∠DAE=∠BAF=90°-∠BAE,
在△AFB和△AED中,
$\left\{\begin{array}{l}{∠F=∠AED}\\{∠FAB=∠DAE}\\{AB=AD}\end{array}\right.$,
∴△AFB≌△AED(AAS),
∴AE=AF=10,S△AFB=S△AED,
∵四边形AFCE是矩形,
∴四边形AFCE是正方形,
∴S正方形AFCE=10×10=100,
∴S四边形ABCD
=S四边形ABCE+S△AED
=S四边形ABCE+S△AFB
=S正方形AFCE
=100;
(2)如图2,过A作AF⊥CD,交CD的延长线于F,
∵AE⊥CD,
∴∠AED=∠F=90°,
∴∠FAE+∠BCD=180°,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠EAF,
∴∠BAD-∠EAD=∠EAF-∠EAD,
∴∠BAE=∠FAD,
在△AEB和△AFD中
$\left\{\begin{array}{l}{∠BAE=∠DAF}\\{∠AEB=∠F}\\{AB=AD}\end{array}\right.$
∴△AEB≌△AFD(AAS),
∴AE=AF=19,BE=DF,
设BE=DF=x,
∵BC=10,CD=6,
∴CE=10-x,CF=6+x,
由勾股定理得;AC2=AE2+CE2=AF2+CF2,
∵AE=AF,
∴CE=CF,
即10-x=6+x,
解得:x=2,
∴CE=CF=8,
∵△AEB≌△AFD
∴S△AEB=S△AFD,
∴S正方形AFCE=$\frac{1}{2}$×8×19+$\frac{1}{2}$×8×19=152
∴S四边形ABCD
=S△AEB+S四边形AECD
=S△AFD+S四边形AECD
=S正方形AFCE
=152.
故答案为:152.
点评 本题考查了全等三角形的性质和判定,矩形的性质和判定,勾股定理,正方形的性质和判定的应用,能综合运用性质进行推理和计算是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | m-2>n-2 | B. | $\frac{m}{2}>\frac{n}{2}$ | C. | -2m>-2n | D. | m+2>n+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:解答题
计算:
(1)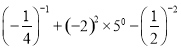
(2)(x2)3÷(x·x2)2
(3)(x-y) 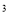 (y-x)
(y-x) 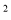 (x-y)+2(x-y)
(x-y)+2(x-y) 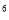
(4)(-2a3)2 -3a2•a4+a8÷a2
(5)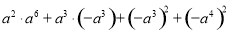
(6)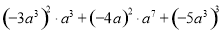
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
DNA是每一个生物携带自身基因的载体,它是遗传物质脱氧核糖核酸的英文简称,DNA分子的直径只有0.0000007cm,则这个数用科学记数法表示是( )
A . 7×10-6 cm B. 0.7×108 cm C. 0.7×10-8 cm D. 7×10-7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论:
把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③b<1;④a>-$\frac{1}{2}$;⑤(a+c)2<b2中正确的有①②⑤(将你认为正确的结论番号都填出来)
如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③b<1;④a>-$\frac{1}{2}$;⑤(a+c)2<b2中正确的有①②⑤(将你认为正确的结论番号都填出来)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com