
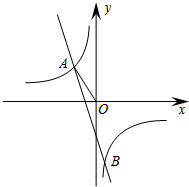
 已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.分析 (1)将点A(-1,a)、B($\frac{1}{3}$,-3)代入反比例函数y=$\frac{k_1}{3x}$中得:-3×$\frac{1}{3}$=(-1)×a=k1,可求k1、a;再将点A(-1,a)、B($\frac{1}{3}$,-3)代入y2=k2x+m中,列方程组求k2、m即可;
(2)根据图象得到一次函数在反比例函数下方时x的取值范围即可求解;
(3)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
解答 解:(1)∵反比例函数y=$\frac{k_1}{3x}$的图象经过B($\frac{1}{3}$,-3),
∴k1=3×$\frac{1}{3}$×(-3)=-3,
∵反比例函数y=$\frac{k_1}{3x}$的图象经过点A(-1,a),
∴a=1.
由直线y2=k2x+m过点A,B得:$\left\{\begin{array}{l}{-{k}_{2}+m=1}\\{\frac{1}{3}{k}_{2}+m=-3}\end{array}\right.$,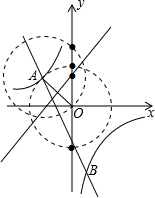 解得$\left\{\begin{array}{l}{{k}_{2}=-3}\\{m=-2}\end{array}\right.$.
解得$\left\{\begin{array}{l}{{k}_{2}=-3}\\{m=-2}\end{array}\right.$.
∴反比例函数关系式为y=-$\frac{1}{x}$,一次函数关系式为y=-3x-2;
(2)k2x+m-$\frac{k_1}{3x}$<0的x的取值范围为-1<x<0或x>$\frac{1}{3}$;
(3)OA=$\sqrt{{1}^{2}+{(-1)}^{2}}$=$\sqrt{2}$,
如图,线段OA的垂直平分线与y轴的交点,有1个,点C的坐标为:(0,1);
以点A为圆心、AO长为半径的圆与y轴的交点,有1个,点C的坐标为:(0,2);
以点O为圆心、OA长为半径的圆与y轴的交点,有2个,点C的坐标为:(0,-$\sqrt{2}$)或(0,$\sqrt{2}$).
故点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,-$\sqrt{2}$)或(0,$\sqrt{2}$)或(0,2)或(0,1).
点评 此题综合考查了待定系数法求函数解析式的方法、等腰三角形的性质等知识,注意分类思想的运用.


科目:初中数学 来源: 题型:选择题
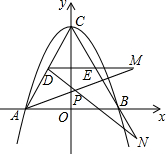 如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,DE是正三角形ABC的中位线.动点M,N分别从D、E出发,沿着射线DE与射线EB方向移动相同的路程,连结AM,DN交于P点.则下列结论:①ac=-3;②AM=DN;③无论M,N处何位置,∠APN的大小始终不变. 其中正确的是( )
如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,DE是正三角形ABC的中位线.动点M,N分别从D、E出发,沿着射线DE与射线EB方向移动相同的路程,连结AM,DN交于P点.则下列结论:①ac=-3;②AM=DN;③无论M,N处何位置,∠APN的大小始终不变. 其中正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
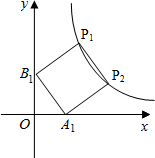 如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).
如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
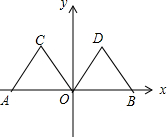 如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com