
| A. | 有理数 | B. | 无理数 | C. | 正数 | D. | 负数 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
| n | 7 | 8 | 9 | 10 |
| m | 2 | 1 | 2 | 2 |
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m | k | k-1 | k | k |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×106 | B. | 3×105 | C. | 0.3×106 | D. | 30×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A. | 平均数 | B. | 众数 | C. | 方差 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有四张不透明的卡片除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图象不经过第四象限的卡片的概率为$\frac{3}{4}$.
如图,有四张不透明的卡片除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图象不经过第四象限的卡片的概率为$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抽取的体检表数n | 50 | 100 | 200 | 400 | 500 | 800 | 1000 | 1200 | 1500 | 2000 |
| 色盲患者的频数m | 3 | 7 | 13 | 29 | 37 | 55 | 69 | 85 | 105 | 138 |
| 色盲患者的频率m/n | 0.060 | 0.070 | 0.065 | 0.073 | 0.074 | 0.069 | 0.069 | 0.071 | 0.070 | 0.069 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
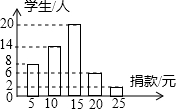 在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行四边形可以看作平移线段得到的图形.如图,将线段AD沿AB的方向平移AB个单位至BC处,就可以得到平行四边形ABCD;或者将线段AB沿AD的方向平移AD个单位至DC处,也可以得到平行四边形ABCD.
平行四边形可以看作平移线段得到的图形.如图,将线段AD沿AB的方向平移AB个单位至BC处,就可以得到平行四边形ABCD;或者将线段AB沿AD的方向平移AD个单位至DC处,也可以得到平行四边形ABCD.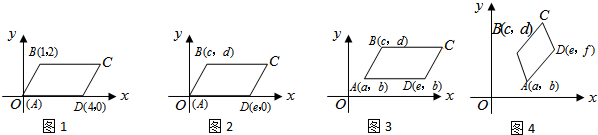
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com