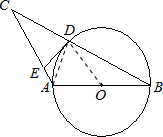
(1)证明:连接OD.
∵OD=OB(⊙O的半径),
∴∠B=∠ODB(等边对等角);
∵AB=AC(已知),
∴∠B=∠C(等边对等角);
∴∠C=∠ODB(等量代换),
∴OD∥AC(同位角相等,两直线平行),
∴∠ODE=∠DEC(两直线平行,内错角相等);
∵DE⊥AC(已知),
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)解:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
∴AD⊥CD;
在Rt△ACD和Rt△DCE中,
∠C=∠C(公共角),
∠CED=∠CDA=90°,
∴Rt△ACD∽Rt△DCE(AA),
∴

=
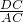
;
又由(1)知,OD∥AC,O是AB的中点,
∴OD是三角形ABC的中位线,
∴CD=

BC;
∵BC=8,AB=5,AB=AC,
∴CE=

.
分析:(1)连接OD,只要证明OD⊥DE即可;
(2)连接AD构造直角三角形ACD,根据相似三角形的判定定理AA判定Rt△ACD∽Rt△DCE,然后由相似三角形的对应边成比例得,

=
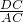
;最后根据三角形中位线的判定与性质求得CD的长度,从而求得CE的长.
点评:本题综合考查了切线的判定与性质、圆周角定理、相似三角形的判定与性质以及三角形中位线的判定与性质.解答(2)时,还可以利用射影定理来求CE的长度.

 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E. (1)证明:连接OD.
(1)证明:连接OD. =
=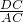 ;
; BC;
BC; .
. =
=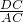 ;最后根据三角形中位线的判定与性质求得CD的长度,从而求得CE的长.
;最后根据三角形中位线的判定与性质求得CD的长度,从而求得CE的长.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为