
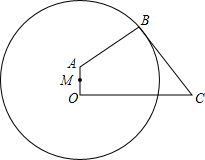
 如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.
如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.分析 (1)利用正切的比设出BH=4x,CH=3x,则BC=5x,作辅助线构建直角三角形证△ABG≌△BCH,利用等量关系列方程求出x的值,从而求出古桥OA与新桥BC的长;
(2)过M作MN⊥BC,构建直角△BNP,证明Rt△BHC∽Rt△BNP,得比例式表示出PN和半径R的长,根据已知古桥两端O和A到该圆上任意一点的距离不少于140m和三角形的三边关系得出不等式组,求出x的取值,最后得出结论.
解答 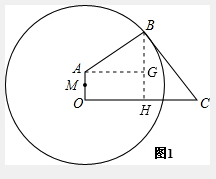 解:(1)如图1,过B作BH⊥OC,垂足为H,
解:(1)如图1,过B作BH⊥OC,垂足为H,
由tan∠BCO=$\frac{4}{3}$,设BH=4x,则CH=3x,BC=5x,
又∵AB⊥BC知,即∠ABH+∠CBH=90°,
又∠BCH+∠CBH=90°,
∴∠ABH=∠BCH,
再过A作AG⊥BH,垂足为G,则∠AGB=∠BHC=90°,
∵AB=BC,
∴△ABG≌△BCH(AAS),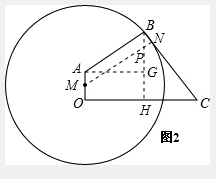
∴BG=CH=3x,AG=BH=4x,
则OH=4x,OA=HG=x,
又OC=210m,即7x=210,x=30,
5x=150,
故古桥OA的长为30m,新桥BC的长的长为150m;
(2)如图2所示,因为OM=xm,故AM=(30-x)m,
过M作MN⊥BC,分别交BC、BH于N、P,
则MN即为保护区半径R,且MP=AB=150,BP=MA=30-x
Rt△BHC∽Rt△BNP,$\frac{PN}{BP}=\frac{CH}{BC}$,则$\frac{PN}{30-x}=\frac{3×30}{5×30}$,PN=18-$\frac{3}{5}$x
①半径R=MN=MP+PN=150+18-$\frac{3}{5}$x=168-$\frac{3}{5}$x
即R=160-$\frac{3}{5}$x(0≤x≤30)
②由题意得:R-OM≥140,即(168-$\frac{3}{5}$x)-x≥140,解得x≤$\frac{35}{2}$
又R-AM≥140,即(168-$\frac{3}{5}$x)-(30-x)≥140,解得x≥5
故有:5≤x≤$\frac{35}{2}$
因为,要使圆面积最大,其半径R最大,而R最大也就是x要取最小值,
故当x=5时,圆面积最大,此时半径为R的值为165m.
点评 此题属于圆的综合题,涉及了全等三角形和相似三角形的判定与性质、三角函数值的知识、不等式组的应用及最大值的求法,综合性较强;有几点技巧需同学们掌握:①利用条件中的三角函数值能求角的度数或利用比值表示边的长;②求极值时也可以利用三边关系列不等式求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
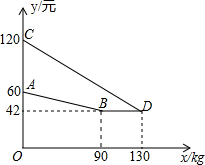 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
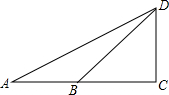 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com