
【题目】如图,四边形ABCD内接于圆O,点E在对角线AC上. 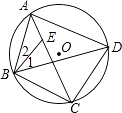
(1)若BC=DC,∠CBD=39°,求∠BCD的度数;
(2)若在AC上有一点E,且EC=BC=DC,求证:∠1=∠2.
【答案】
(1)解:∵BC=CD,
∴ ![]() =
= ![]() ,
,
∴∠BAC=∠DAC=∠CBD=39°,
∴∠BAD=78°,
∵四边形ABCD为圆内接四边形,
∴∠BCD=102°;
(2)解:∵BC=CD,
∴∠CBD=∠CDB,又∠BAC=∠BDC,
∴∠CBD=∠BAE,
∴∠CEB=∠BAE+∠2,
∵CB=CE,
∴∠CBE=∠CEB,
∴∠BAE+∠2=∠CBD+∠1,
∴∠1=∠2.
【解析】(1)根据BC=CD,得到 ![]() =
= ![]() ,求出∠BAD=78°,根据圆内接四边形的性质计算即可;(2)根据等腰三角形的性质和三角形的外角的性质解答即可.
,求出∠BAD=78°,根据圆内接四边形的性质计算即可;(2)根据等腰三角形的性质和三角形的外角的性质解答即可.
【考点精析】掌握等腰三角形的性质和圆周角定理是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,解答下列问题: 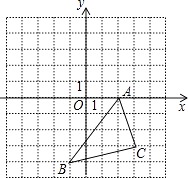
(1)分别写出A、B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(3)求出线段B1A所在直线l的函数解析式,并写出在直线l上从B1到A的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:①单项式5×103x2的系数是5;②当x分别取2和-2时,多项式x3-2x的值互为相反数 ;③多项式﹣3a2b+7a2b2-2ab+1的次数是9;④若单项式3x2ym+2与xn-1y的和仍然是一个单项式,则m、n的值分别是-1和3;⑤几个有理数相乘,当负因数的个数为奇数时,积为负数.其中判断正确的有________________ .(将正确答案的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )
A. 495 B. 497 C. 501 D. 503
查看答案和解析>>
科目:初中数学 来源: 题型:
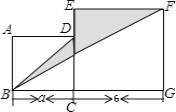
【题目】如图,正方形ABCD和正方形ECGF的边长分别为a和6,
(1) 写出表示阴影部分面积的代数式(结果要求化简);
(2) 求![]() 时,阴影部分的面积.
时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
材料:将一组正整数1,2,3,4,5,…按下面的方法进行排列:

我们规定:正整数2的位置记为(1,2),正整数8的位置记为(2,5).
问题:(1)若一个数a的位置记作(4,3),则a=________;
(2)正整数2017的位置可记为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com