
����Ŀ���ڡ�ABC�У�AB��AC����A��60�㣬��D���߶�BC���е㣬��EDF��120�㣬DE���߶�AB�ཻ�ڵ�E��DF���߶�AC����AC���ӳ��ߣ��ཻ�ڵ�F��
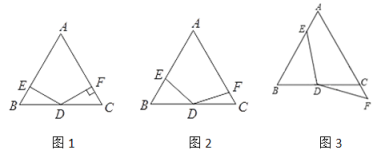
��1����ͼ1����DF��AC������ΪF��֤����DE��DF
��2����ͼ2������EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F��DE��DF��Ȼ������˵�����ɣ�
��3����ͼ3������EDF�����Ƶ�D˳ʱ����תһ���ĽǶȣ�ʹDF���߶�AC���ӳ����ཻ�ڵ�F��DE��DF��Ȼ������˵�����ɣ�
���𰸡���1������������2��������Ȼ����.��DE��DF������������3����Ȼ������DE��DF��������
��������
��1�����������ȫ�������ε��������ж�����ϵȱ�����������֤����BED�ա�CFD��ASA��������֤��DE��DF��
��2������������ȡAC�е�G,����DG,�̶���ȫ�������ε��������ж�����ϵȱ�����������֤����EDG�ա�FDC��ASA��������֤��DE��DF��
��3�����������D��DN��AC��N,DM��AB��M, �̶���ȫ�������ε��������ж�����ϵȱ�����������֤����DME�ա�DNF��ASA��������֤��DE��DF��
�⣺��1����AB=AC����A=60����
���ABC�ǵȱ�������,����B=��C=60��,
��D��BC���е�,
��BD=CD,
�ߡ�EDF=120����DF��AC��
���FDC=30��,
���EDB=30����
���BED�ա�CFD��ASA��,
��DE=DF.
��2��ȡAC�е�G,����DG,����ͼ,
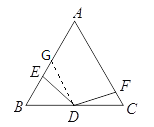
��DΪBC���е�,
��DG=![]() AC=BD=CD,
AC=BD=CD,
���BDG�ǵȱ�������,
���GDE+��EDB=60��,
�ߡ�EDF=120��,
���FDC+��EDB=60��,
���EDG=��FDC,
���EDG�ա�FDC��ASA��,
��DE=DF��
��������Ȼ����.
��3������ͼ,����D��DN��AC��N,DM��AB��M,
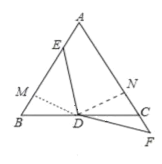
���DME=��DNF=90��,
�ɣ�1����֪��B=��C=60��,
���NDC=��BDM=30��,DM=DN,
���MDN=120��,����NDF=��MDE,
���DME�ա�DNF��ASA��,
��DE=DF,
����Ȼ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʻ��������Ҫ�����������Ƚ�ͨ����ʵʩ��ijУ��ѧ����ʵ��С��Ͷ���Щ��ͨ������˽������ȫУ��������˲���ѧ������������Ϊ���֣�A���dz��˽⣬B���Ƚ��˽⣬C�������˽⣬D����̫�˽⣬ʵ��С��Ѵ˴ε��������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ��
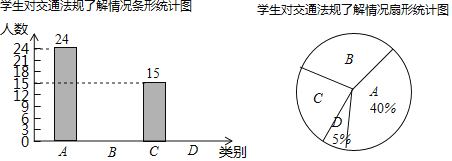
����ͼ��������Ϣ����������⣺
��1�����ι�����������ѧ��������ͳ��ͼ��C����Ӧ���ε�Բ�ĽǶ�����������
��2����ȫ����ͳ��ͼ��
��3����У����800��ѧ��������������Ϣ���������ȫУѧ���ж���Щ��ͨ�������dz��˽������ж�������
��4��ͨ���˴ε��飬��ѧ����ʵ��С���ѧ���Խ�ͨ�������˸������ʶ��ѧУ�������ڵļס��ҡ���������λѧ���������ȡ����ѧ���μ�������ͨ���澺���������б�����״ͼ�ķ������������ѧ��ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
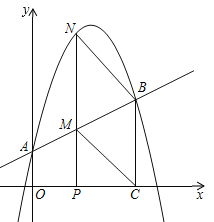
����Ŀ����ͼ��������![]() ��y�ύ��A�㣬����A��ֱ���������߽�����һ��B������B��BC��x�ᣬ����Ϊ��C(3��0).
��y�ύ��A�㣬����A��ֱ���������߽�����һ��B������B��BC��x�ᣬ����Ϊ��C(3��0).
��1����ֱ��AB�ĺ�����ϵʽ��
��2������P���߶�OC�ϴ�ԭ�������ÿ��һ����λ���ٶ���C�ƶ�������P��PN��x�ᣬ��ֱ��AB�ڵ�M�����������ڵ�N. ���P�ƶ���ʱ��Ϊt�룬MN�ij���Ϊs����λ����s��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3�����ڣ�2���������£������ǵ�P���O����C�غϵ������������CM��BN����tΪ��ֵʱ���ı���BCMNΪƽ���ı��Σ��ʶ��������tֵ��ƽ���ı���BCMN�Ƿ����Σ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y����x2+2x+3��ͼ��x���ڵ�A��B����A�ڵ�B����ࣩ�����ѵ�B����ƽ��m��m��0������λ���ȵõ�B1������B1����ƽ��n��n��0������λ���ȣ�����ö��κ���ͼ���ϵĵ�B2�غϣ�����B1����ƽ�ƣ�n+2������λ���ȣ�����ö��κ���ͼ���ϵĵ�B3�غϣ���n��ֵΪ��������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����֪����AOCD��ƽ��ֱ������ϵxOy�У���CAO��60����OA��2��B�������Ϊ��2��0��������M��ÿ��2����λ���ȵ��ٶ���A��C��B�˶���M�㲻���A����B�غϣ������˶�ʱ��Ϊt�룮
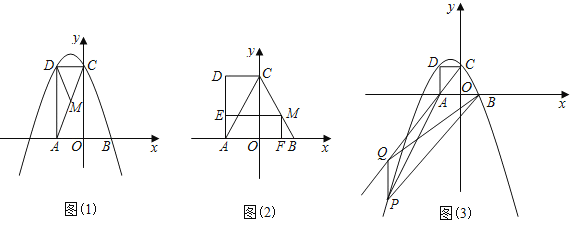
��1����B��C��D����������߽���ʽ��
��2����P�ڣ�1���е��������ϣ���MΪAC�е�ʱ������PAM�ա�PDM�����P�����ꣻ
��3������M��CB���˶�ʱ����ͼ��2������M��ME��AD��MF��x�ᣬ����ֱ�ΪE��F�������AEMF����ABC�ص��������ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
��4����ͼ��3����P�ڣ�1���е��������ϣ�Q��CA�ӳ����ϵ�һ�㣬��P��Q������ڵ��������ڣ�Q��A��λ��ֱ��BPͬ��IJ�ͬ���㣬����P��x��ľ���Ϊd����QPB�����Ϊ2d�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
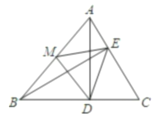
����Ŀ����ͼ������ABC�У�AD��BC��D��BE��AC��E��MΪAB�ߵ��е㣬����ME��MD��ED����AB=10����DBE=30��������EDM�����Ϊ____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A����C��![]() ���е㣬�����н��ۣ���OC��AE����EC��BC���ۡ�DAE����ABE����AC��OE��������ȷ���У�������
���е㣬�����н��ۣ���OC��AE����EC��BC���ۡ�DAE����ABE����AC��OE��������ȷ���У�������
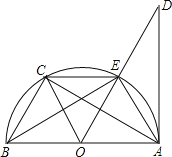
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
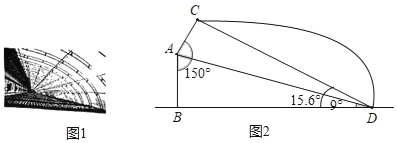
����Ŀ������ʡ����Ϊ�ٽ�ũҵ��չ���ӿ�ũ�彨�裬�ƻ������˽�һ�����ֹ�װ��ʽ�����ͼ1��ʾ�߶�AB��BD�ֱ�Ϊ�����ǽ�ߺͿ�ȣ�AC��ʾ���°�ij�����֪ǽ��ABΪ3�ף�ǽ���뱣�°����ɵĽǡ�BAC��150�㣬�ڵ�D�����A�㡢C������Ƿֱ�Ϊ9�㣬15��6�㣬��ͼ2��ʾ���°�AC�ij��Ƕ����ף�����ȷ��0.1�ף����ο����ݣ�sin9���0.16��cos9���0.99��tan9���0��16��sin15.6���0.27��cos15.6���0.96��tan15.6���0.28��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֪��
����֪��![]() ���ҶԳ���Ϊֱ��
���ҶԳ���Ϊֱ��![]() ��
��

��1����������ߵĽ���ʽ��
��2����![]() �ǵ����������������ϵ�һ�㣬��
�ǵ����������������ϵ�һ�㣬��![]() ��������ʱ�����
��������ʱ�����![]() �����ꣻ
�����ꣻ
��3����ͼ2����![]() ���������ϵ�һ�����㣬����
���������ϵ�һ�����㣬����![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ����
����![]() ʱ��ֱ��д����
ʱ��ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com