
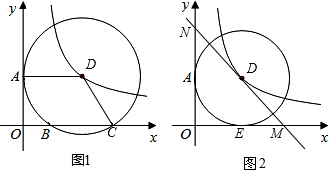
���� ��1���ѵ㣨4��$\sqrt{3}$������y=$\frac{k}{x}$��x��0���õ����ۣ�
��2����ͼ1������BD����D��DG��BC��G���������ߵ����ʵõ�DA��y�ᣬ�õ��ı���AOGD�Ǿ��Σ��Ƴ�DG=OA�����D�ĺ�����Ϊx������������Ϊ $\frac{4\sqrt{3}}{x}$�������ı���ABCDΪ���Σ��õ�BC=DA=DB=DC���뾶����֤�á�DBCΪ�ȱ������Σ��������Ǻ����Ķ��弴�ɵõ����ۣ�
��3����ͼ2������DA��DB���ɡ�D��x�������ڵ�E���õ�DE��OM�������ı���AOED�������Σ����D�İ뾶=a���õ�AD=DE=a���������������ε����ʼ��ɵõ����ۣ�
��� �⣺��1���߷���������y=$\frac{k}{x}$��x��0��ͼ���㣨4��$\sqrt{3}$����
��$\sqrt{3}$=$\frac{k}{4}$��
��k=4$\sqrt{3}$��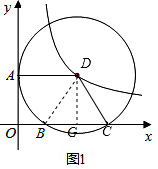
�෴������������ʽΪy=$\frac{4\sqrt{3}}{x}$��
��2����ͼ1������BD����D��DG��BC��G��
�ߡ�D��y�������ڵ�A��
��DA��y�ᣬ
���ı���AOGD�Ǿ��Σ�
��DG=OA��
���D�ĺ�����Ϊx������������Ϊ $\frac{4\sqrt{3}}{x}$��
����D��DG��OC��G��
���ı���ABCDΪ���Σ�
��BC=DA=DB=DC���뾶����
���DBCΪ�ȱ������Σ�
��Rt��DBG�У���DBG=60�㣬DB=DA=x��DG=$\frac{\sqrt{3}}{2}$x��
��$\frac{\sqrt{3}}{2}$x=$\frac{4\sqrt{3}}{x}$��
��ã�x=��2$\sqrt{2}$����ֵ��ȥ����
��DA=BC=DC=2$\sqrt{2}$��
���D�������ǣ�2$\sqrt{2}$$\sqrt{3}$����
��3��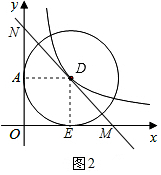 ��ͼ2������DA��DB��
��ͼ2������DA��DB��
�ߡ�D��x�������ڵ�E��
��DE��OM��
���ı���AOED�������Σ�
���D�İ뾶=a��
��AD=DE=a��
��AD��OM��DE��ON��
���ADN�ס�OMN�ס�EMD��
��$\frac{AD}{OM}=\frac{DN}{MN}$��$\frac{DE}{ON}=\frac{DM}{MN}$��
��$\frac{AD}{OM}+\frac{DE}{ON}=\frac{DN}{MN}+\frac{DM}{MN}$��
��$\frac{a}{OM}+\frac{a}{ON}=1$��
��$\frac{1}{OM}$+$\frac{1}{ON}$=$\frac{1}{a}$����ֵ����
��$\frac{1}{OM}$+$\frac{1}{ON}$Ϊ��ֵ��
���� ���⿼���˷������������ۺ������Լ����Ρ�Բ�����ʺ������ε��ж������������ε��ж������ʣ���֪ʶ���������ν��˼������ǽ���ؼ���


 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ��֪ʶ��չ
��һ��֪ʶ��չ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����O�ǡ�ABC�����Բ������AOB=110�㣬���ACB�Ķ����ǣ�������
��ͼ����O�ǡ�ABC�����Բ������AOB=110�㣬���ACB�Ķ����ǣ�������| A�� | 55�� | B�� | 70�� | C�� | 125�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22017-1 | B�� | 22017+1 | C�� | 22016-1 | D�� | 22016+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24x2y3 | B�� | 24xy2 | C�� | 12x2y2 | D�� | 12xy2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
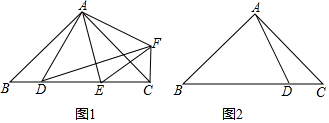
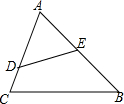 ��ͼ����ABC�У�EΪAB�е㣬AB=6��AC=4.5����ADE=��B����CD=��������
��ͼ����ABC�У�EΪAB�е㣬AB=6��AC=4.5����ADE=��B����CD=��������| A�� | $\frac{3}{2}$ | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com