
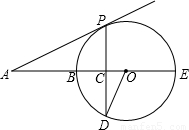
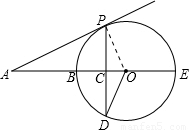
 (1)证明:连接OP,
(1)证明:连接OP,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《圆》(13)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《圆》(05)(解析版) 题型:选择题
 cm的⊙O上一点,现有动点P、Q同时从点A出发,分别以3cm/秒,1cm/秒的速度沿圆周作顺时针和逆时针方向运动,那么下列结论错误的是( )
cm的⊙O上一点,现有动点P、Q同时从点A出发,分别以3cm/秒,1cm/秒的速度沿圆周作顺时针和逆时针方向运动,那么下列结论错误的是( )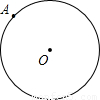
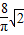 cm
cm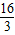 秒
秒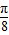 cm
cm查看答案和解析>>
科目:初中数学 来源:2002年湖北省黄冈市中考数学试卷(解析版) 题型:选择题
 cm的⊙O上一点,现有动点P、Q同时从点A出发,分别以3cm/秒,1cm/秒的速度沿圆周作顺时针和逆时针方向运动,那么下列结论错误的是( )
cm的⊙O上一点,现有动点P、Q同时从点A出发,分别以3cm/秒,1cm/秒的速度沿圆周作顺时针和逆时针方向运动,那么下列结论错误的是( )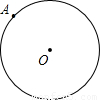
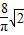 cm
cm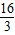 秒
秒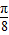 cm
cm查看答案和解析>>
科目:初中数学 来源:2002年湖北省黄冈市中考数学试卷(解析版) 题型:填空题
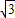 cm,将△ABC绕点B旋转至△A′BC′的位置,且使点A、B、C′三点在一条直线上,则点A经过的最短路线的长度是 .
cm,将△ABC绕点B旋转至△A′BC′的位置,且使点A、B、C′三点在一条直线上,则点A经过的最短路线的长度是 .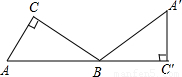
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com