
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】试题分析:(1)、根据“可分四边形”和“可分角”的定义得出答案;(2)、根据角平分线的性质得出∠DAC=∠CAB=30°,∠DCA=150°-∠ACB,然后根据角度之间的关系得出∠ADC=∠ACB,从而说明△ACD和△ABC相似,从而得出结论;(3)、根据“可分四边形”和“可分角”的性质得出∠DAC=∠CAB, ![]() ,从而说明△ACD和△ABC相似,根据相似得出∠ACB=∠D=90°,然后根据勾股定理求出AB的长度,结合
,从而说明△ACD和△ABC相似,根据相似得出∠ACB=∠D=90°,然后根据勾股定理求出AB的长度,结合![]() 得出AD的长度.
得出AD的长度.
试题解析:(1)![]()
(2)∵AC平分∠DAB,∠DAB=60° ∴∠DAC=∠CAB=30° ∵∠DCB=150°
∴∠DCA=150°-∠ACB
在△ADC中,∠ADC=180°- ∠DAC- ∠DCA =180°-30°-(150°-∠ACB)=∠ACB
∴△ACD∽△ABC ∴![]() ∴
∴![]() , 即证四边形ABCD为“可分四边形”
, 即证四边形ABCD为“可分四边形”
(3)∵四边形ABCD为“可分四边形”,∠DAB为“可分角”∴AC平分∠DAB, ![]()
即∠DAC=∠CAB, ![]() ∴△ACD∽△ABC ∴∠ACB=∠D=90°
∴△ACD∽△ABC ∴∠ACB=∠D=90°
在Rt△ACB中AB= ![]() ∵
∵![]() ∴AD=
∴AD=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知,AB∥CD,AB,CD被直线l所截,点P是l上的一动点,连接PA,PC.
(1)如图①,当P在AB,CD之间时,求证:∠APC=∠A+∠C; 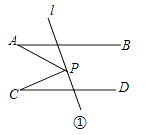
(2)如图②,当P在射线ME上时,探究∠A,∠C,∠APC的关系并证明; 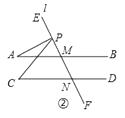
(3)如图③,当P在射线NF上时,直接写出∠A,∠C,∠APC三者之间关系. 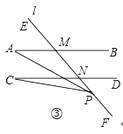
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2 , 如此进行下去,得到四边形AnBnCnDn . 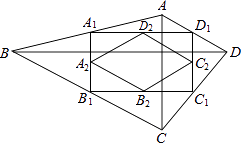
(1)求证:四边形A1B1C1D1是矩形;
(2)四边形A3B3C3D3是形;
(3)四边形A1B1C1D1的周长为;
(4)四边形AnBnCnDn的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从二次函数y=ax2+bx+c的图象(如图)中观察得出了下面五条信息:①c<0;②abc>0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0.你认为其中正确的信息是( )

A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.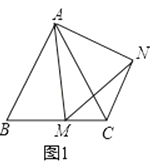
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.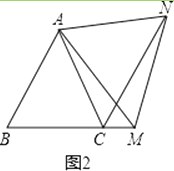
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com