
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据勾股定理的逆定理以及直角三角形的定义,验证四组条件中数据是否满足“较小两边平方的和等于最大边的平方”由此即可得出结论.
解答 解:①∵a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$),
∵($\frac{1}{3}$)2+($\frac{1}{4}$)2≠($\frac{1}{5}$);
∴满足①的三角形不是直角三角形;
②a=6,b=8,c=10,
∵62+82=102,
∴满足②的三角形是直角三角形;
③a=7,b=24,c=25,
∵72+242=252,
∴满足③的三角形为直角三角形;
④a=2,b=3,c=4.
∵22+32≠42,
∴满足④的三角形不是直角三角形.
综上可知:满足②③的三角形均为直角三角形.
故选B.
点评 本题考查了勾股定理的逆定理以及直角三角形的定义,解题的关键是根据勾股定理的逆定理和直角三角形的定义验证四组条件.本题属于基础题,难度不大,解决该题型题目时,套入数据验证“较小两边平方的和是否等于最大边的平方(或寻找三角形中是否有一个角为直角)”是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
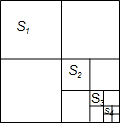 【阅读】求值:1+2+22+23+…+22016
【阅读】求值:1+2+22+23+…+22016查看答案和解析>>
科目:初中数学 来源: 题型:填空题
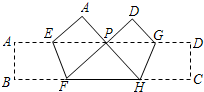 如图,把宽为3cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为16cm,则长方形ABCD的面积为48cm2.
如图,把宽为3cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为16cm,则长方形ABCD的面积为48cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com