
”¾ĢāÄæ”æµćOĪŖÖ±ĻßABÉĻŅ»µć£¬ŌŚÖ±ĻßABĶ¬²ąČĪ×÷ÉäĻßOC”¢OD£¬Ź¹µĆ”ĻCOD=90”ć
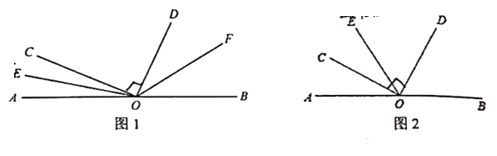
£Ø1£©ČēĶ¼1£¬¹żµćO×÷ÉäĻßOE£¬µ±OEĒ”ŗĆĪŖ”ĻAOCµÄ½ĒĘ½·ÖĻߏ±£¬Įķ×÷ÉäĻßOF£¬Ź¹µĆOFĘ½·Ö”ĻBOD£¬Ōņ”ĻEOFµÄ¶ČŹżŹĒ__________¶Č£»
£Ø2£©ČēĶ¼2£¬¹żµćO×÷ÉäĻßOE£¬µ±OEĒ”ŗĆĪŖ”ĻAODµÄ½ĒĘ½·ÖĻߏ±£¬Ēó³ö”ĻBODÓė”ĻCOEµÄŹżĮæ¹ŲĻµ£»
£Ø3£©¹żµćO×÷ÉäĻßOE£¬µ±OCĒ”ŗĆĪŖ”ĻAOEµÄ½ĒĘ½·ÖĻߏ±£¬Įķ×÷ÉäĻßOF£¬Ź¹µĆOFĘ½·Ö”ĻCOD£¬Čō”ĻEOC=3”ĻEOF£¬Ö±½ÓŠ“³ö”ĻAOEµÄ¶ČŹż
”¾“š°ø”æ£Ø1£©135”ć£»£Ø2£©”ĻBOD=2”ĻCOE£»£Ø3£©67.5”ć.
”¾½āĪö”æ
£Ø1£©ÓÉ”ĻCOD=90”ć£¬Ōņ”ĻAOC+”ĻBOD=90”ć£¬ÓÉOEĘ½·Ö”ĻAOC£¬OFĘ½·Ö”ĻBOD£¬µĆ”ĻCOE+”ĻDOF=45”ć£¬¼“æÉĒó³ö”ĻEOFµÄ¶ČŹż£»
£Ø2£©ÓÉĢāŅāµĆ³ö”ĻBOD+”ĻAOC=90”ć£¬”ĻBOD=180”ć![]() ”ĻAOD£¬ŌŁÓɽĒĘ½·ÖĻߵĶØŅå½ųŠŠ¼ĘĖć£¬¼“æÉµĆ³ö½į¹ū£»
”ĻAOD£¬ŌŁÓɽĒĘ½·ÖĻߵĶØŅå½ųŠŠ¼ĘĖć£¬¼“æÉµĆ³ö½į¹ū£»
£Ø3£©ÓɽĒĘ½·ÖĻ߶ØŅåµĆ³ö”ĻAOC=”ĻCOE£¬”ĻCOF=”ĻDOF=45”ć£¬ŌŁÓÉ”ĻBOD+”ĻAOC=90”ć£¬Éč”ĻEOF=x£¬Ōņ”ĻEOC=3x£¬”ĻCOF=4x£¬øł¾ŻĢāŅāµĆ³ö·½³Ģ£¬½ā·½³Ģ¼“æÉ£®
½ā£ŗ£Ø1£©ČēĶ¼£ŗ
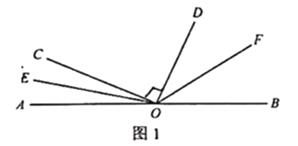
”ß”ĻCOD=90”ć£¬
”ą”ĻAOC+”ĻBOD=90”ć£¬
”ßOEĘ½·Ö”ĻAOC£¬OFĘ½·Ö”ĻBOD£¬
”ą”ĻCOE+”ĻDOF=![]() £¬
£¬
”ą”ĻEOF=”ĻCOE+”ĻCOD+”ĻDOF=45”ć+90”ć=135”ć£»
¹Ź“š°øĪŖ£ŗ135”ć£»
£Ø2£©”ĻBOD=2”ĻCOE£»
ĄķÓÉČēĻĀ£ŗČēĶ¼£¬
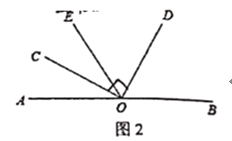
”ß”ĻCOD=90”ć£®
”ą”ĻBOD+”ĻAOC=90”ć£¬
”ßOEĘ½·Ö”ĻAOD£¬
”ą”ĻAOE=”ĻDOE=![]() ”ĻAOD£¬
”ĻAOD£¬
Ó֔ߔĻBOD=180”ć![]() ”ĻAOD£¬
”ĻAOD£¬
”ą”ĻCOE=”ĻAOE![]() ”ĻAOC
”ĻAOC
=![]() ”ĻAOD
”ĻAOD![]() £Ø90”ć
£Ø90”ć![]() ”ĻBOD£©
”ĻBOD£©
=![]() £Ø180”ć
£Ø180”ć![]() ”ĻBOD£©
”ĻBOD£©![]() 90”ć+”ĻBOD
90”ć+”ĻBOD
=![]() ”ĻBOD£¬
”ĻBOD£¬
”ą”ĻBOD=2”ĻCOE£»
£Ø3£©ČēĶ¼£¬
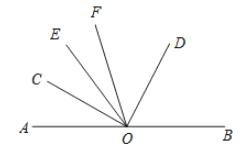
”ßOCĪŖ”ĻAOEµÄ½ĒĘ½·ÖĻߣ¬OFĘ½·Ö”ĻCOD£¬
”ą”ĻAOC=”ĻCOE£¬”ĻCOF=”ĻDOF=45”ć£¬
”ß”ĻEOC=3”ĻEOF£¬
Éč”ĻEOF=x£¬Ōņ”ĻEOC=3x£¬
”ą”ĻCOF=4x£¬
”ą”ĻAOE=2”ĻCOE=6x£¬”ĻDOF=4x£¬
”ß”ĻCOD=90”ć£¬
”ą4x+4x=90”ć£¬
½āµĆ£ŗx=11.25”ć£¬
”ą”ĻAOE=6”Į11.25”ć=67.5”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”放ĪŹĢāĒé¾°”æĄūÓĆČż½ĒŠĪµÄĆ껿ĻąµČĄ“Ēó½āµÄ·½·ØŹĒŅ»ÖÖ³£¼ūµÄµČ»ż·Ø£¬“Ė·½·ØŹĒĪŅĆĒ½ā¾ö¼øŗĪĪŹĢāµÄĶ¾¾¶Ö®Ņ»£®
ĄżČē£ŗÕÅĄĻŹ¦øųŠ”“ĻĢį³öÕāŃłŅ»øöĪŹĢā£ŗ
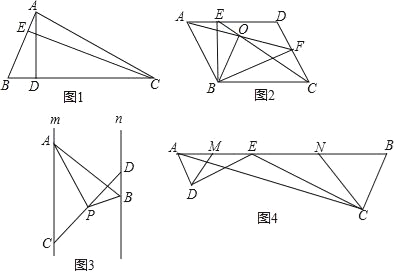
ČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬AB=3£¬AD=6£¬ĪŹ”÷ABCµÄøßADÓėCEµÄ±ČŹĒ¶ąÉŁ£æ
Š”“ĻµÄ¼ĘĖćĖ¼Ā·ŹĒ£ŗ
øł¾ŻĢāŅāµĆ£ŗS”÷ABC=![]() BCAD=
BCAD=![]() ABCE£®
ABCE£®
“Ó¶ųµĆ2AD=CE£¬”ą![]()
ĒėŌĖÓĆÉĻŹö²ÄĮĻÖŠĖł»żĄŪµÄ¾ŃéŗĶ·½·Ø½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©”¾Ąą±ČĢ½¾æ”æ
ČēĶ¼2£¬ŌŚABCDÖŠ£¬µćE”¢F·Ö±šŌŚAD£¬CDÉĻ£¬ĒŅAF=CE£¬²¢Ļą½»ÓŚµćO£¬Į¬½ÓBE”¢BF£¬
ĒóÖ¤£ŗBOĘ½·Ö½ĒAOC£®
£Ø2£©”¾Ģ½¾æŃÓÉģ”æ
ČēĶ¼3£¬ŅŃÖŖÖ±Ļßm”Īn£¬µćA”¢CŹĒÖ±ĻßmÉĻĮ½µć£¬µćB”¢DŹĒÖ±ĻßnÉĻĮ½µć£¬µćPŹĒĻ߶ĪCDÖŠµć£¬ĒŅ”ĻAPB=90”ć£¬Į½Ę½ŠŠĻßm”¢n¼äµÄ¾ąĄėĪŖ4£®ĒóÖ¤£ŗPAPB=2AB£®
£Ø3£©”¾ĒØŅĘÓ¦ÓĆ”æ
ČēĶ¼4£¬EĪŖAB±ßÉĻŅ»µć£¬ED”ĶAD£¬CE”ĶCB£¬“¹×ć·Ö±šĪŖD£¬C£¬”ĻDAB=”ĻB£¬AB=![]() £¬BC=2£¬AC=
£¬BC=2£¬AC=![]() £¬ÓÖŅŃÖŖM”¢N·Ö±šĪŖAE”¢BEµÄÖŠµć£¬Į¬½ÓDM”¢CN£®Ēó”÷DEMÓė”÷CENµÄÖܳ¤Ö®ŗĶ£®
£¬ÓÖŅŃÖŖM”¢N·Ö±šĪŖAE”¢BEµÄÖŠµć£¬Į¬½ÓDM”¢CN£®Ēó”÷DEMÓė”÷CENµÄÖܳ¤Ö®ŗĶ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĒóÖŖ֊ѧӊŅ»æéĖıߊĪµÄæÕµŲABCD£¬ČēĻĀĶ¼ĖłŹ¾£¬Ń§Š£¼Ę»®ŌŚæÕµŲÉĻÖÖÖ²²ŻĘ¤£¬¾²āĮæ”ĻA=90”ć£¬AB=3m£¬BC=12m£¬CD=13m£¬DA=4m£¬ČōĆæĘ½·½ĆײŻĘ¤ŠčŅŖ250ŌŖ£¬ĪŹŃ§Š£ŠčŅŖĶ¶Čė¶ąÉŁ×Ź½šĀņ²ŻĘ¤£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
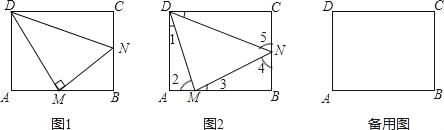
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬µćM“ÓAµć³ö·¢ŌŚĻ߶ĪABÉĻ×÷ŌČĖŁŌĖ¶Æ£Ø²»ÓėA”¢BÖŲŗĻ£©£¬Ķ¬Ź±µćN“ÓBµć³ö·¢ŌŚĻ߶ĪBCÉĻ×÷ŌČĖŁŌĖ¶Æ£®
£Ø1£©ČēĶ¼1£¬ČōMĪŖABÖŠµć£¬ĒŅDM”ĶMN£®ĒėŌŚĶ¼ÖŠÕŅ³öĮ½¶ŌĻąĖĘČż½ĒŠĪ£ŗ
¢Ł”” ”””×”” ””_£¬¢Ś”” ”””×”” ””£¬Ń”ŌńĘäÖŠŅ»¶Ō¼ÓŅŌÖ¤Ć÷£»
£Ø2£©¢ŁČēĶ¼2£¬ČōAB=5£¬BC=3µćMµÄĖŁ¶ČĪŖ1øöµ„Ī»³¤¶Č/Ćė£¬µćNµÄĖŁ¶ČĪŖ![]() øöµ„Ī»³¤¶Č/Ćė£¬ŌĖ¶ÆµÄŹ±¼äĪŖtĆė£®µ±tĪŖŗĪÖµŹ±£¬”÷DAMÓė”÷MBNĻąĖĘ£æĒėĖµĆ÷ĄķÓÉ£»
øöµ„Ī»³¤¶Č/Ćė£¬ŌĖ¶ÆµÄŹ±¼äĪŖtĆė£®µ±tĪŖŗĪÖµŹ±£¬”÷DAMÓė”÷MBNĻąĖĘ£æĒėĖµĆ÷ĄķÓÉ£»
¢ŚČē¹ū°ŃµćNµÄĖŁ¶ČøÄĪŖaøöµ„Ī»³¤¶Č/Ćė£¬ĘäĖüĢõ¼ž²»±ä£¬ŹĒ·ń“ęŌŚaµÄÖµ£¬Ź¹µĆ”÷DAMÓė”÷MBNŗĶ”÷DCNÕāĮ½øöČż½ĒŠĪ¶¼ĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öaµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬![]() £¬EĪŖBDÖŠµć£¬ŃÓ³¤CDµ½µćF£¬Ź¹
£¬EĪŖBDÖŠµć£¬ŃÓ³¤CDµ½µćF£¬Ź¹![]() £®
£®
![]() ĒóÖ¤£ŗ
ĒóÖ¤£ŗ![]()
![]() ĒóÖ¤£ŗĖıߊĪABDFĪŖĘ½ŠŠĖıߊĪ
ĒóÖ¤£ŗĖıߊĪABDFĪŖĘ½ŠŠĖıߊĪ
![]() Čō
Čō![]() £¬
£¬![]() £¬
£¬![]() £¬ĒóĖıߊĪABDFµÄĆ껿
£¬ĒóĖıߊĪABDFµÄĆ껿

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬PĪŖ”÷ABCĖłŌŚĘ½ĆęÉĻŅ»µć£¬ĒŅ”ĻAPB£½”ĻBPC£½”ĻCPA£½120”ć£¬ŌņµćP½Š×÷”÷ABCµÄ·ŃĀķµć£®
(1)Čē¹ūµćPĪŖČń½Ē”÷ABCµÄ·ŃĀķµć£¬ĒŅ”ĻABC£½60”ć.
¢ŁĒóÖ¤£ŗ ”÷ABP”×”÷BCP£»
¢ŚČōPA£½3£¬PC£½4£¬ĒóPBµÄ³¤£»
(2)ČēĶ¼¢Ś£¬ŅŃÖŖČń½Ē”÷ABC£¬·Ö±šŅŌAB£¬ACĪŖ±ßĻņĶā×÷Õż”÷ABEŗĶÕż”÷ACD£¬CEŗĶBDĻą½»ÓŚµćP£¬Į¬½ÓAP.
¢ŁĒó”ĻCPDµÄ¶ČŹż£»
¢ŚĒóÖ¤£ŗµćPĪŖ”÷ABCµÄ·ŃĀķµć£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŅ»ŌŖ¶ž“Ī·½³Ģax2+bx+c=0£Øa”Ł0£©ÖŠ£¬ĻĀĮŠĖµ·Ø£ŗ
¢ŁČōa+b+c=0£¬Ōņb2©4ac£¾0£»
¢ŚČō·½³ĢĮ½øłĪŖ©1ŗĶ2£¬Ōņ2a+c=0£»
¢ŪČō·½³Ģax2+c=0ÓŠĮ½øö²»ĻąµČµÄŹµøł£¬Ōņ·½³Ģax2+bx+c=0±ŲÓŠĮ½øö²»ĻąµČµÄŹµøł£»
¢ÜČōb=2a+c£¬Ōņ·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµøł£®ĘäÖŠÕżČ·µÄÓŠ£Ø””””£©
A. ¢Ł¢Ś¢Ū B. ¢Ł¢Ś¢Ü C. ¢Ś¢Ū¢Ü D. ¢Ł¢Ś¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¾ÅÄź¼¶ÓŠ1200Ćūѧɜ£¬ŌŚĢåÓżæ¼ŹŌĒ°Ė껜³éČ”²æ·Öѧɜ½ųŠŠĢųÉž²āŹŌ£¬øł¾Ż²āŹŌ³É¼ØÖĘ×÷ĮĖĻĀĆęĮ½øöĶ³¼ĘĶ¼.Ēėøł¾ŻĻą¹ŲŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ

£Ø¢ń£©±¾“Ī²Ī¼ÓĢųÉž²āŹŌµÄѧɜČĖŹżĪŖ___________£¬Ķ¼¢ŁÖŠ![]() µÄÖµĪŖ___________£»
µÄÖµĪŖ___________£»
£Ø¢ņ£©Ē󱾓Īµ÷²é»ńČ”µÄŃł±¾Źż¾ŻµÄĘ½¾łŹż”¢ÖŚŹżŗĶÖŠĪ»Źż£»
£Ø¢ó£©øł¾ŻŃł±¾Źż¾Ż£¬¹Ą¼ĘøĆŠ£¾ÅÄź¼¶ĢųÉž²āŹŌÖŠµĆ3·ÖµÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Į½ĢõÖ±ĻßAB£¬CDĻą½»ÓŚµćO£¬ĒŅ”ĻAOC£½”ĻAOD£¬ÉäĻßOM“ÓOBæŖŹ¼ČĘOµćÄꏱÕė·½ĻņŠż×Ŗ£¬ĖŁ¶ČĪŖ15”ć/s£¬ÉäĻßONĶ¬Ź±“ÓODæŖŹ¼ČĘOµćĖ³Ź±Õė·½ĻņŠż×Ŗ£¬ĖŁ¶ČĪŖ12”ć/s£¬ŌĖ¶ÆŹ±¼äĪŖtĆė£Ø0£¼t£¼12£¬±¾Ģā³öĻֵĽĒ¾łŠ”ÓŚĘ½½Ē£©
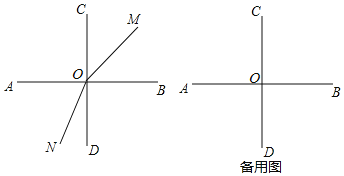
£Ø1£©Ķ¼ÖŠŅ»¶ØÓŠ”” ””øöÖ±½Ē£»µ±t£½2Ź±£¬”ĻMONµÄ¶ČŹżĪŖ”” ””£¬”ĻBONµÄ¶ČŹżĪŖ”” ””£»
£Ø2£©ČōOEĘ½·Ö”ĻCOM£¬OFĘ½·Ö”ĻNOD£¬µ±”ĻEOFĪŖÖ±½ĒŹ±£¬ĒėĒó³ötµÄÖµ£»
£Ø3£©µ±ÉäĻßOMŌŚ”ĻCOBÄŚ²æ£¬ĒŅ![]() ŹĒ¶ØÖµŹ±£¬ĒótµÄȔֵ·¶Ī§£¬²¢Ēó³öÕāøö¶ØÖµ£®
ŹĒ¶ØÖµŹ±£¬ĒótµÄȔֵ·¶Ī§£¬²¢Ēó³öÕāøö¶ØÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com