
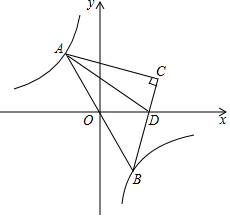
 如图,等腰直角三角形ABC的直角顶点C在第一象限,顶点A、B分别在函数y=$\frac{8}{x}$图象的两个分支上,且AB经过原点O,BC与x轴相交于点D,连接AD,已知AD平分四边形AODC的面积.
如图,等腰直角三角形ABC的直角顶点C在第一象限,顶点A、B分别在函数y=$\frac{8}{x}$图象的两个分支上,且AB经过原点O,BC与x轴相交于点D,连接AD,已知AD平分四边形AODC的面积.分析 (1)根据反比例函数图象的对称性和三角线的面积公式得到S△ABO=2S△ACD.即BD=2CD;
(2)如图,过点B作BE⊥x轴于E,过点C作CF⊥x于F,连接OC,构建全等三角形△OBE≌△CDF,结合该全等三角形的对应边相等得到:BE=CD,OE=CF,由$\frac{BE}{CF}$=$\frac{BD}{CD}$=2推知BE=2OE.设OE=a,则BE=2a,所以B(a,-2a),根据反比例函数图象上点的坐标特征和反比例函数图象的对称性来求点A的坐标即可.
解答 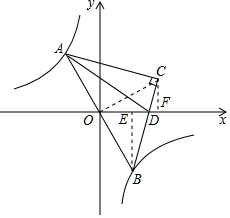 (1)证明:∵函数y=$\frac{8}{x}$图象关于原点对称,
(1)证明:∵函数y=$\frac{8}{x}$图象关于原点对称,
∴OA=OB,
∴S△AOD=S△BOD.
∵AD平分四边形AODC的面积,
∴S△AOD=S△ACD.
∴S△ABO=2S△ACD.
∴BD=2CD;
(2)解:如图,过点B作BE⊥x轴于E,过点C作CF⊥x于F,连接OC,则∠BEO=∠OFC=90°.
∵△ABC是等腰直角三角形,OA=OB,
∴∠BOC=90°,OC=$\frac{1}{2}$AB=OB,
∴∠BOE+∠COF=90°,而∠BOE+∠OBE=90°,
∴∠OBE=∠COF,
∵在△OBE与△CDF中,$\left\{\begin{array}{l}{∠BEO=∠OFC}\\{OBE=∠COF}\\{OB=CO}\end{array}\right.$,
∴△OBE≌△CDF(AAS),
∴BE=CD,OE=CF,
∵∠DBE=∠DCF,
∴cos∠DBE=cos∠DCF,
∴$\frac{BE}{BD}$=$\frac{CF}{CD}$,
∵$\frac{BE}{CF}$=$\frac{BD}{CD}$=2,
∴BE=2CF,
∴BE=2OE.
设OE=a,则BE=2a,
∴B(a,-2a),
∴a•(-2a)=-8,
解得a=2,
∴B(2,-4),
∴A(-2,4).
点评 本题考查了反比例函数综合题,综合运用反比例函数图象上点的坐标特征,反比例函数图象关于原点对称,全等三角形的判定与性质以及三角形面积的求法等知识点,难度不大,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
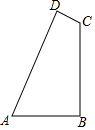 如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )
如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )| A. | 12 | B. | 6+$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{6}$+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
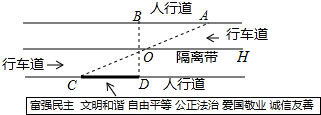 杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:
杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
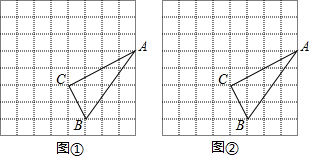 如图,小方格的边长为1,△ABC为格点三角形.
如图,小方格的边长为1,△ABC为格点三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:
某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com