
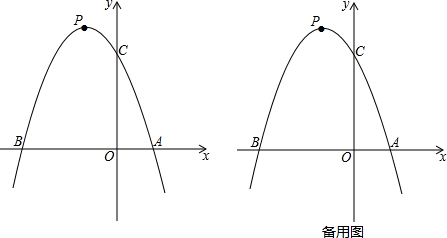
分析 (1)根据抛物线经过A(1,0),B(-3,0)两点,与y轴交于点C,且OB=OC,可以求得点C的坐标,根据两点式可以求得抛物线的解析式;
(2)根据第一问中求出的A、B、C各点的坐标,可以求出BP、CP、BC的长度,根据勾股定理的逆定理可以得到△BCP野史直角三角形,对应边的比与△OAC的对应边的比相等,从而可以求得两个三角形相似;
(3)根据题意画出相应的图形,再根据题意,可以分别表示出各边之间的关系,再根据相似三角形对应边的比相等,从而可以得到两个方程,联立方程组,从而可以求得点M的值.
解答 解:(1)∵OB=OC=3,B(-3,0),
∴C(0,3).
设抛物线的解析式y=a(x+3)(x-1),
∵抛物线与y轴交于点C(0,3),
∴-3a=3.
解得a=-1.
∴抛物线的解析式为y=-(x+3)(x-1)=-x2-2x+3.
(2)△AOC与△PCB相似.
理由:如下图一所示: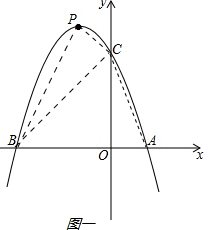
∵y=-x2-2x+3=-(x+1)2+4,
∴点P的坐标为(-1,4),
∵OA=1,OC=3,
∴BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=3$\sqrt{2}$,PC=$\sqrt{1+(3-4)^{2}}$=$\sqrt{2}$,PB=$\sqrt{(-1+3)^{2}+{4}^{2}}$=2$\sqrt{5}$.
∴BC2+PC2=PB2.
∴∠PCB=∠AOC=90°.
∴BC:OC=PC:OA.
∴△PCB∽△AOC.
(3)如下图二所示:
当△MPN与△BPH相似时.
则PH:MN=BH:NP,
∵PH:BH=2:1,
∴MN:NP=2:1.
∴MN2:MP2=4:5.
设M(x,y).
∵B(-3,0),P(-1,4),设过点B、P的直线为:y=kx+b.
∴y=2x+6.
∴点M到直线BP的距离MN为:$\frac{|2x-y+6|}{\sqrt{{2}^{2}+(-1)^{2}}}$.
则MN2=$\frac{(2x-y+6)^{2}}{5}$.
MP2=(x+1)2+(y-4)2
又∵y=-x2-2x+3,
∴$\left\{\begin{array}{l}{\frac{(2x-y+6)^{2}}{5}:[(x+1)^{2}+(y-4)^{2}]}\\{y=-{x}^{2}-2x+3}\end{array}\right.$=4:5
解得,x=$\frac{1}{3}$,y=$\frac{20}{9}$.
故点M的坐标为($\frac{1}{3}$,$\frac{20}{9}$).
点评 本题考查二次函数的解析式的求法、三角形相似、点到直线的距离,解答本题的关键是可以根据题意画出相应的图形,再根据题意灵活变化,建立等量关系,找出所求问题的条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )| A. | 随C、D的运动位置而变化,且最大值为4 | |
| B. | 随C、D的运动位置而变化,且最小值为2 | |
| C. | 随C、D的运动位置长度保持不变,等于2 | |
| D. | 随C、D的运动位置而变化,没有最值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
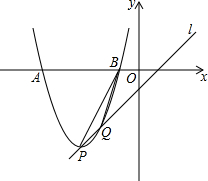 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
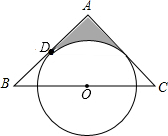 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 7cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com