
【题目】如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6). 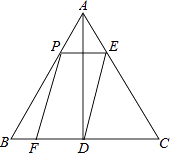
(1)求线段PE的长.(用含x的代数式表示)
(2)当四边形PEDF为菱形时,求x的值.
【答案】
(1)解:∵PE∥BC,
∴△APE∽△ABC,
又∵△ABC是等边三角形,
∴△APE是等边三角形,
∴PE=AP=x(0<x<6);
(2)解:∵四边形PEDF为菱形,
∴PE=DE=x,
又∵△APE是等边三角形,则AE=PE,
∴AE=DE,
∴∠DAC=∠ADE,
又∵∠ADE+∠EDC=∠DAC+∠C=90°,
∴∠EDC=∠C,
∴DE=EC,
∴DE=EC=AE= ![]() AC=
AC= ![]() AB=3,
AB=3,
即x=3.
【解析】(1)由PE与BC平行,得到三角形APE与三角形ABC相似,根据三角形ABC为等边三角形,得到三角形APE为等边三角形,可得出PE=AP=x;(2)若四边形PEDF为菱形,得到PE=DE=x,由三角形APE为等边三角形得到AE=PE,可得出AE=DE,利用等边对等角得到∠DAC=∠ADE,利用等式的性质得到∠EDC=∠C,利用等角对等边得到DE=EC,即可求出x的值;
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F. 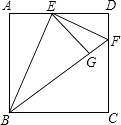
(1)若∠ABE:∠BFC=n,则n=;
(2)当E运动到AD中点时,求线段GF的长;
(3)若限定F仅在线段CD上(含端点)运动,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
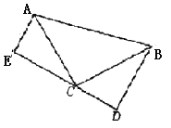
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
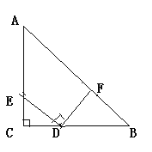
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
西瓜质量(单位:千克) | 5.4 | 5.3 | 5.0 | 4.8 | 4.4 | 4.0 |
西瓜数量(单位:个) | 1 | 2 | 3 | 2 | 1 | 1 |
(1)这10个西瓜质量的众数和中位数分别是 和 ;
(2)计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
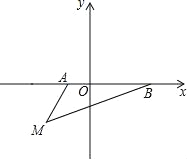
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
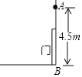
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
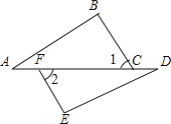
【题目】如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有_____.
①∠E=∠B;②ED=BC;③AB=EF;④AF=CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com