练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，二次函数y=ax2+bx+c的图象经过（-1，0）、（0,3），下列结论中错误的是（  ）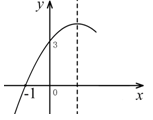

    A．abc＜0 B．9a+3b+c=0 C．a-b="-3"  D． 4ac﹣b2＜0 

    B．

    解析试题分析：A、∵抛物线对称轴x=-＞0，∴ab＜0，又∵抛物线与y轴交于正半轴，∴c＞0，∴abc＜0，正确，故本选项不符合题意；
    B、观察图象，由于没有给出对称轴方程，所以不能得出x=3时，函数值的符号，所以9a+3b+c不一定等于0，即9a+3b+c=0不一定正确，故本选项符合题意；
    C、∵二次函数y=ax2+bx+c的图象经过（-1，0）、（0，3），
    ∴，
    ②代入①，整理，得a-b=-3，正确，故本选项不符合题意；
    D、∵抛物线与x轴有两个交点，∴b2-4ac＞0，即4ac-b2＜0，正确，故本选项不符合题意．
    故选B．
    考点：二次函数的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    在“美丽广西，清洁乡村”活动中，李家村村长提出了两种购买垃圾桶方案；方案1：买分类垃圾桶，需要费用3000元，以后每月的垃圾处理费用250元；方案2：买不分类垃圾桶，需要费用1000元，以后每月的垃圾处理费用500元；设方案1的购买费和每月垃圾处理费共为y1元，交费时间为x个月；方案2的购买费和每月垃圾处理费共为y2元，交费时间为x个月．

    （1）直接写出y1、y2与x的函数关系式；
    （2）在同一坐标系内，画出函数y1、y2的图象；
    （3）在垃圾桶使用寿命相同的情况下，哪种方案省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（　　）

    A．c＞0 B．2a+b=0C．b2﹣4ac＞0 D．a﹣b+c＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，在矩形ABCD中，AB=2，点E在边AD上，∠ABE=45°，BE=DE，连接BD，点P在线段DE上，过点P作PQ∥BD交BE于点Q，连接QD．设PD=x，△PQD的面积为y，则能表示y与x函数关系的图象大致是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是（     ）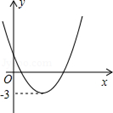

    A．k＜－3 B．k＞－3 C．k＜3 D．k＞3

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    已知关于x的二次函数y＝x2－2x＋c的图像上有两点A(x1，y1)，B(x2，y2)，若x1<1<x2且x1＋x2＝2，则y1与y2的大小关系是

    A．y1<y2B．y1>y2C．y1＝y2D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    已知二次函数的图象与x轴的一个交点为（1,0），则它与x轴的另一个交点坐标是

    A．（1，0） B．（－1，0） C．（2，0） D．（－2，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，已知边长为4的正方形ABCD，E是BC边上一动点(与B、C不重合)，连结AE，作EF⊥AE交∠BCD的外角平分线于F，设BE＝x，△ECF的面积为y，下列图象中，能表示y与x的函数关系的图象大致是（   ）

    A．          B．
    C．        D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    已知二次函数y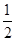＝－x2－7x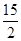＋，若自变量x分别取x1，x2，x3，且0<x1<x2<x3，则对应的函数值y1，y2，y3的大小关系正确的是(　　)

    A．y1>y2>y3B．y1<y2<y3
    C．y2>y3>y1D．y2<y3<y1

    查看答案和解析>>

    同步练习册答案