
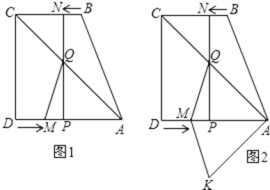
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,求 出AC的长.
【答案】(1)8﹣2t,2+t;(2)t=2;(3)![]()
【解析】
(1)由DM=2t,根据AM=AD-DM即可求出AM=8-2t;先证明四边形CNPD为矩形,得出DP=CN=6-t,则AP=AD-DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得6-t=8-(6-t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6-t-2t=8-(6-t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.
解:(1)如图1.
∵四边形CNPD为矩形 ∴DP=CN=BC﹣BN=6﹣t,
∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),解得t=2,
(3)①存在时刻t=1,使四边形AQMK为菱形.理由如下:
∵NP⊥AD,QP=PK
∴当PM=PA时有四边形AQMK为菱形
∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°,∴∠CAD=45°
∴四边形AQMK为正方形,则CD=AD,
∵AD=8,∴CD=8,
∴AC=![]() .故答案为:
.故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
A. 当a=1时,函数图象过点(-1,1)
B. 当a=-2时,函数图象与x轴没有交点
C. 若a>0,则当x≥1时,y随x的增大而减小
D. 若a<0,则当x≤1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+2k﹣4=0有两个不相等的实数根.
(1)求k的取值范围:
(2)若k为正整数,且该方程的根都是整数,求k的值及该方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
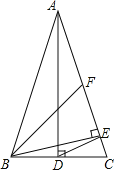
【题目】如图,在△ABC中,AB=AC═12,AD⊥BC,BE⊥AC,F为AC中点,连接BF、DE,当BE2﹣DE2最大时,则DE长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)(1)如图①,点E、F、G、H分别在平行四边形ABCD的边AB、BC、CD、DA上,连结EF、FG、GH、HE,将△AEH、△BFE、△CGF、△DHG分别沿EF、FG、GH、HE折叠,折叠后的图形恰好能拼成一个无重叠、无缝隙的矩形.若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(拓展)(2)参考图②,四边形ABCD是平行四边形,![]() ,当按图①的方式折叠后的图形能拼成一个无重叠、无缝隙的正方形时,则
,当按图①的方式折叠后的图形能拼成一个无重叠、无缝隙的正方形时,则![]() ___________.
___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为![]() 元的台灯以
元的台灯以![]() 元售出,平均每月能售出
元售出,平均每月能售出![]() 个,调查表明:这种台灯的售价每上涨
个,调查表明:这种台灯的售价每上涨![]() 元,其销售量就减少
元,其销售量就减少![]() 个.
个.
![]() 为了实现平均每月
为了实现平均每月![]() 元的销售利润,这种台灯的售价应定为多少?这时应进台灯个?
元的销售利润,这种台灯的售价应定为多少?这时应进台灯个?
![]() 如果商场要想每月的销售利润最多,这种台灯的售价又将定为多少?这时应进台灯多个?
如果商场要想每月的销售利润最多,这种台灯的售价又将定为多少?这时应进台灯多个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
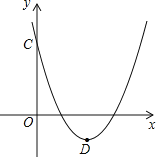
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市采暖季出现 PM2.5 污染,小明妈妈收集了一个月(30 天)的 PM2.5 污染指数,记录如下:(单位:μg/m3)说明:0-50 优,51-100 良,101-150 轻度污染,151-200 中度污染,201-250 重度污染,251 以上严重污染.117,171,170, 208,192,120,243,256,56,115,166,155,156,187,114,49,55, 95,148,160,15,31,62,174,183,162,131,112,96,71对这 30 个数据按组距 50 进行分组,并统计整理,绘制了如下尚不完整的统计图表:
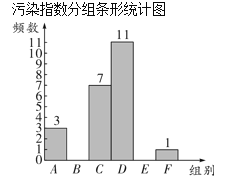
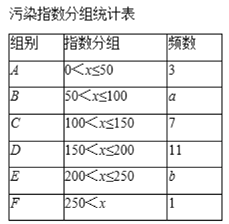
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)这 30 天 PM2.5 污染指数的中位数落在 组;
(4)若一个采暖季为 120 天,请估计空气污染指数不低于 100 的天数(结果取整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com