练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
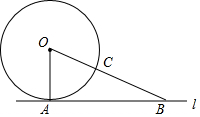
    4．如图，直线l是⊙O的切线，A为切点，B为直线l上一点，连接OB交⊙O于点C．若AB=12，OA=5，则BC的长为（　　）
    A．5B．6C．7D．8

    分析 根据勾股定理，可得OB的长，根据线段的和差，可得答案．

    解答 解：由勾股定理，得
    OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=13，
    CB=OB-OC=13-5=8，
    故选：D．

    点评 本题考查了切线的性质，利用勾股定理得出OB的长是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．下表为我省大同市5个空气质量监测站点对某日空气中PM2.5浓度（单位：μg/m3）的检测数据，则这组数据的中位数为（　　）
    检测站点果树杨云冈宾馆大同大学安家小村教育学院
    PM2.5浓度76μg/m380μg/m397μg/m394μg/m393μg/m3
    A．97μg/m3B．80μg/m3C．94μg/m3D．93μg/m3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

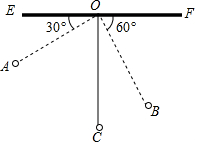    15．如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在OA的位置时俯角∠EOA=30°，在OB的位置时俯角∠FOB=60°，若OC⊥EF，点A比点B高7cm．求：
    （1）单摆的长度（$\sqrt{3}$≈1.7）；
    （2）从点A摆动到点B经过的路径长（π≈3.1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，直线a∥b，∠1=72°，则∠2的度数是（　　）
    A．118°B．108°C．98°D．72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，在菱形ABCD中，∠DAB=60°，AB=2，则菱形ABCD的面积为2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．我们规定：当k，b为常数，k≠0，b≠0，k≠b时，一次函数y=kx+b与y=bx+k互为交换函数．例如：y=4x+3的交换函数为y=3x+4．一次函数y=kx+2与它的交换函数图象的交点横坐标为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．2+$\frac{3x+3}{8}$＞3-$\frac{x+7}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．我市某工艺厂为配合伦敦奥运，设计了一款成本为20元/件的工艺品投入市场进行试销，得到如数据：
    销售单价x
    （元/件）    		…30405060…
    每天销售量
    y（件）    		…500400300200…

    （1）把表中x、y的各组对应值作为点的坐标，在如图的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
    （2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润为9000元？（利润=销售总价-成本总价）
    （3）根据要求，试销该工艺品每天获得的利润不低于8000元，每天销售量不低于350件，试确定销售单价x（元/件）的取值范围，并求出工艺厂试销该工艺品每天获得的最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，在△ABC中，DE是AC的垂直平分线，△ABC的周长为27cm，△BCE的周长为18cm，则AD的长为4.5cm．

    查看答案和解析>>

    同步练习册答案