
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).

(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
【答案】(1)y=-x2+![]() x+1;(2)4;(3)(
x+1;(2)4;(3)(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据题意得出B点坐标,再利用待定系数法求出抛物线解析式;
(2)首先表示出P,E点坐标,再利用PE=PD-ED,结合二次函数最值求法进而求出PE的最大值;
(3)根据题意可得:PE=BC,则-x2+4x=3,进而求出Q点的横坐标,再利用直线上点的坐标性质得出答案.
试题解析:(1)∵BC⊥x轴,垂足为点C(4,0),且点B在直线y=![]() x+1上,
x+1上,
∴点B的坐标为:(4,3),
∵抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴![]() ,
,
解得: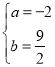 ,
,
故抛物线的解析式为:y=-x2+![]() x+1;
x+1;
(2)如图所示:设动点P的坐标为;(x,-x2+![]() x+1),
x+1),
则点E的坐标为:(x,![]() x+1),
x+1),
∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=(-x2+![]() x+1)-(
x+1)-(![]() x+1)
x+1)
=-x2+4x
=-(x-2)2+4,
则当x=2时,PE的最大值为:4;
(3)∵PC与BE互相平分,
∴PE=BC,
∴-x2+4x=3,即x2-4x+3=0,
解得:x1=1,x2=3,
∵点Q分别时PC,BE的中点,且点Q在直线y=![]() x+1,
x+1,
∴①当x=1时,点Q的横坐标为:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ),
),
②当x=3时,点Q的横坐标为:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ),
),
综上所述,点Q的坐标为:(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图①,在菱形ABCD中,∠ABC=120°,点M,N分别在AD,CD上,且∠MBN=60°,试判断四边形DMBN是否为“等邻边四边形”?请说明理由.
(2)如图②,在矩形ABCD中,AB=8,BC=12.5,点E在BC上,且BE=6,在矩形ABCD内或边上,确定一点P,使四边形ABEP为最大面积的“等邻边四边形”,若能实现,请求出最大面积;若不能实现,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 为正方形
为正方形![]() 的边
的边![]() 上任意一点,在正方形内部做等腰直角
上任意一点,在正方形内部做等腰直角![]() .
.


(1)如图1,若![]() ,则
,则![]() _________(请直接写出答案)
_________(请直接写出答案)
(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①补全图形1;
②证明:四边形ECHF为平行四边形.
(3)在(2)的条件下,连接![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为![]() ,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形
,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形![]() 的面积是________.
的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),

(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒. 问此车是否超过了该路段16米/秒的限制速度?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com