
【题目】我市部分学生参加了全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
请根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.
【答案】(1)全市共有300名学生参加本次竞赛决赛,最低分在20-39之间,最高分在120-140之间;(2)65%;(3)中位数落在60-79分数段内;(4)如“120分以上有12人;60至79分数段的人数最多”等,答案不唯一.
【解析】
(1)把图表中的人数加起来即可;
(2)60分以上的人数有195人,用195除以总人数得获奖率;
(3)由中位数概念判断;
(4)答案不唯一,写出正确信息即可.
解:(1)37+68+95+56+32+12=300,即全市共有300名学生参加本次竞赛决赛,最低分在20-39之间,最高分在120-140之间;
(2)60分以上的人数有95+56+32+12=195人,则本次决赛共有195人获奖,获奖率为![]() ×100%=65%;
×100%=65%;
(3)将这组数据按从小到大排列为,由于有偶数个数,取最中间两个数的平均数,第150、151位都是60-79分数段内,则决赛成绩的中位数落在60-79分数段内;
(4)如“120分以上有12人;60至79分数段的人数最多”等.


科目:初中数学 来源: 题型:
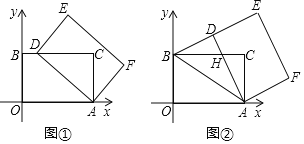
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() =( )
=( )

A. ﹣![]() B. ﹣
B. ﹣![]() C. ﹣
C. ﹣![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA和OB是⊙O的半径,OB=2,OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R.
(1)求证:RP=RQ;
(2)若OP=PQ,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于圆O,∠BOC=120°,AD为圆O的直径.AD交BC于P点且PB=1,PC=2,则AC的长为( )
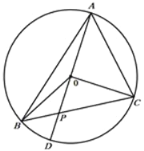
A. ![]() B.
B. ![]() C. 3D. 2
C. 3D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
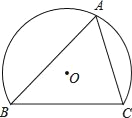
【题目】如图,弓形ABC中,∠BAC=60°,BC=2![]() ,若点P在优弧BAC上由点B向点C移动,记△PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围为_____.
,若点P在优弧BAC上由点B向点C移动,记△PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com