
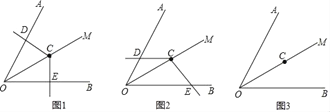
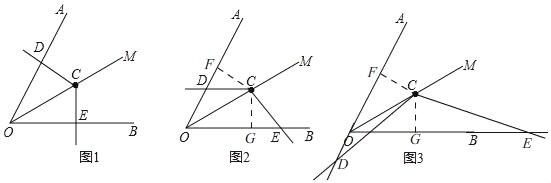
����Ŀ����ͼ����֪��AOB=60��������AOB��ƽ����OM����һ��C����һ��120���ǵĶ������C�غϣ����������߷ֱ���ֱ��OA��OB�ཻ�ڵ�D��E��
��1������DCE�Ƶ�C��ת��CD��OA��ֱʱ����ͼ1���������OE+OD��OC��������ϵ��˵�����ɣ�
��2������DCE�Ƶ�C��ת��CD��OA����ֱʱ������ͼ2��λ�ã���1���еĽ����Ƿ������˵�����ɣ�
��3������DCE�Ƶ�C��ת��CD��OA�ķ����ӳ����ཻʱ�����������Ƿ����������ͼ3�л���ͼ�Σ��������������֤���������������߶�OD��OE��OC֮������������������ϵ����д����IJ��룬������֤����
���𰸡���1��OD+OE=![]() OC��֤�������������2����1���н�����Ȼ���������������������3����1���н��۲�����������ΪOE��OD=
OC��֤�������������2����1���н�����Ȼ���������������������3����1���н��۲�����������ΪOE��OD=![]() OC��֤���������.
OC��֤���������.
��������
(1)���жϳ���OCE=60��,����������ǵ����Ǻ����ó�OD=![]() OC, ͬ����OE=
OC, ͬ����OE=![]() OC ,�����ó�����;(2)ͬ(1)�ķ����ó�OF+OG=
OC ,�����ó�����;(2)ͬ(1)�ķ����ó�OF+OG=![]() OC,���жϳ���CFD�ա�CGE,�ó�DF=EG,�����ݵ���������⣻(3)ͬ(2)�ķ����ó����ۼ���.
OC,���жϳ���CFD�ա�CGE,�ó�DF=EG,�����ݵ���������⣻(3)ͬ(2)�ķ����ó����ۼ���.
�⣺��1����OM����AOB�Ľ�ƽ���ߣ����AOC=��BOC=![]() ��AOB=30�㣬
��AOB=30�㣬
��CD��OA�����ODC=90�㣬���OCD=60�㣬���OCE=��DCE����OCD=60�㣬
��Rt��OCD��OD=OCcos30��=![]() OC��
OC��
ͬ����OE=![]() OC����OD+OE=
OC����OD+OE=![]() OC��
OC��
��2����1���н�����Ȼ���������ɣ�
����C��CF��OA��F��CG��OB��G��
���OFC=��OGC=90�㣬�ߡ�AOB=60�㣬���FCG=120�㣬
ͬ��1���ķ����ã�OF=![]() OC��OG=
OC��OG=![]() OC��
OC��
��OF+OG=![]() OC����CF��OA��CG��OB���ҵ�C����AOB��ƽ����OM��һ�㣬��CF=CG��
OC����CF��OA��CG��OB���ҵ�C����AOB��ƽ����OM��һ�㣬��CF=CG��
�ߡ�DCE=120�㣬��FCG=120�㣬���DCF=��ECG�����CFD�ա�CGE����DF=EG��
��OF=OD+DF=OD+EG��OG=OE��EG�� ��OF+OG=OD+EG+OE��EG=OD+OE��
��OD+OE=![]() OC��
OC��
��3����1���н��۲�����������Ϊ��OE��OD=![]() OC��
OC��
���ɣ�����C��CF��OA��F��CG��OB��G�����OFC=��OGC=90�㣬
�ߡ�AOB=60�㣬���FCG=120�㣬
ͬ��1���ķ����ã�OF=![]() OC��OG=
OC��OG=![]() OC����OF+OG=
OC����OF+OG=![]() OC��
OC��
��CF��OA��CG��OB���ҵ�C����AOB��ƽ����OM��һ�㣬
��CF=CG���ߡ�DCE=120�㣬��FCG=120�㣬���DCF=��ECG�����CFD�ա�CGE����DF=EG��
��OF=DF��OD=EG��OD��OG=OE��EG����OF+OG=EG��OD+OE��EG=OE��OD��
��OE��OD=![]() OC��
OC��


 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B=90�㣬AB=12��BC=24������P�ӵ�A��ʼ�ر�AB���յ�B��ÿ��2����λ���ȵ��ٶ��ƶ�������Q�ӵ�B��ʼ�ر�BC��ÿ��4����λ���ȵ��ٶ����յ�C�ƶ��������P��Q�ֱ�ӵ�A��Bͬʱ��������ô��PBQ�����S�����ʱ��t��s����α仯��д��������ϵʽ��t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
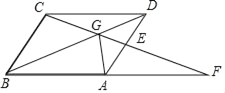
����Ŀ����֪����ABCD�У�AB=8����G�ǶԽ���BD��һ�㣬CG��BA���ӳ����ڵ�F��
��1����֤��CG2=GEGF��
��2�����DG=![]() GB����AG��BF����cos��F��
GB����AG��BF����cos��F��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ķ���
�Ķ���![]() ��
��![]() �ֱ�������
�ֱ�������![]() �ı�
�ı�![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() ������
������![]() �ĶԽ���
�ĶԽ���![]() ��.
��.

��1����֤��![]() ��
��
��2����![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() ��������
��������![]() ���ܳ���
���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ������������ijˮ���깺��һ����ˮ��������Ϊ 20 Ԫ/ǧ�ˣ��ۼ۲����� 20 Ԫ/ǧ�ˣ��Ҳ����� 32 Ԫ/ǧ�ˣ�����������������ָ�ˮ��һ��������� y��ǧ�����������ۼ� x��Ԫ/ǧ�����������±���ʾ��һ�κ�����ϵ��
������ y��ǧ�ˣ� | �� | 34.8 | 32 | 29.6 | 28 | �� |
�ۼ� x��Ԫ/ǧ�ˣ� | �� | 22.6 | 24 | 25.2 | 26 | �� |
(1)ij������ˮ�����ۼ�Ϊ 23.5 Ԫ/ǧ�ˣ������ˮ������������
(2)���ij����������ˮ������ 150 Ԫ����ô����ˮ�����ۼ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ1800m2����������̻������żס����������̶����.��֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ400 m2������̻�ʱ���ӱ��Ҷ�����4��.
��1����ס��������̶�ÿ��������̻�������ֱ��Ƕ���m2��
��2����ѧУÿ���踶���ӵ��̻�������0.4��Ԫ���Ҷ�Ϊ0.25��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����8��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ٶȷֱ�Ϊ100km/h��akm/h��0��a��100���������ֱ�����sǧ������ͬʱ��������ͬһ��������ǰ�У���ʻһ��ʱ�������һ����ԭ�ٶ�ԭ·���أ�ֱ������һ������ʱ����ֹͣ���ڴ˹����У�����֮��ľ���y��km������ʻʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ������˵������a��60����b��2����c��b+![]() ������s��60����b��
������s��60����b��![]() ������˵����ȷ���ǣ�������
������˵����ȷ���ǣ�������

A.�٢ڢ�B.�ڢۢ�C.�٢ڢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
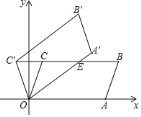
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�ƽ���ı���
�У�ƽ���ı���![]() �Ķ���
�Ķ���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ����ƽ���ı���
����ƽ���ı���![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת�õ�ƽ���ı���
��ʱ�뷽����ת�õ�ƽ���ı���![]() ������
������![]() ����
����![]() ���ӳ�����ʱ���߶�
���ӳ�����ʱ���߶�![]() ��
��![]() �ڵ�
�ڵ�![]() �����߶�
�����߶�![]() �ij���Ϊ________��
�ij���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ����ǻ�У�����裬ij����Ϊ�Ե�ѧУ�ɹ�һ��![]() �����ͺŵ�һ����������г����鷢�֣�ÿ��
�����ͺŵ�һ����������г����鷢�֣�ÿ��![]() ��һ����ļ۸��ÿ��
��һ����ļ۸��ÿ��![]() ��һ����ļ۸��
��һ����ļ۸��![]() ��Ԫ������
��Ԫ������![]() ��Ԫǡ���ܹ���
��Ԫǡ���ܹ���![]() ��
��![]() ��һ�����
��һ�����![]() ��
��![]() ��һ���.
��һ���.
��1���ж�Ԫһ�η����������⣺��ÿ��![]() �ͺ�
�ͺ�![]() ��һ����ļ۸���Ƕ�����Ԫ��
��һ����ļ۸���Ƕ�����Ԫ��
��2��������Ҫ�������ٴβɹ�![]() �ͺ�
�ͺ�![]() ��һ�����
��һ�����![]() �ף���ʱÿ��
�ף���ʱÿ��![]() ������ļ۸��ԭ������
������ļ۸��ԭ������![]() ��ÿ��
��ÿ��![]() ��һ����ļ۸�.���ٴβɹ�
��һ����ļ۸�.���ٴβɹ�![]() ��һ���
��һ���![]() �ף���ô�������ٻ���ҪͶ�������Ԫ��
�ף���ô�������ٻ���ҪͶ�������Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com