
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= ![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2. 
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
【答案】
(1)解:过点A作AD⊥x轴,垂足为D

由A(n,6),C(﹣2,0)可得,
OD=n,AD=6,CO=2
∵tan∠ACO=2
∴ ![]() =2,即
=2,即 ![]() =2
=2
∴n=1
∴A(1,6)
将A(1,6)代入反比例函数,得m=1×6=6
∴反比例函数的解析式为 ![]()
将A(1,6),C(﹣2,0)代入一次函数y=kx+b,可得
![]()
解得 ![]()
∴一次函数的解析式为y=2x+4
(2)解:由  可得
可得 ![]()
![]()
解得x1=1,x2=﹣3
∵当x=﹣3时,y=﹣2
∴点B坐标为(﹣3,﹣2)
【解析】本题主要考查了反比例函数与一次函数的交点问题,解决问题的关键是掌握待定系数法求函数解析式.求反比例函数与一次函数的交点坐标时,把两个函数关系式联立成方程组求解,若方程组有解,则两者有交点,若方程组无解,则两者无交点.(1)先过点A作AD⊥x轴,根据tan∠ACO=2,求得点A的坐标,进而根据待定系数法计算两个函数解析式;(2)先联立两个函数解析式,再通过解方程求得交点B的坐标即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】解不等式组: .
.
请结合题意,完成本题的解答.
(1)解不等式①,得 ,依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来.
![]()
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
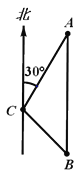
【题目】如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C处80海里,轮船沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到达航线AB的距离;
(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=![]() .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,
,![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点.如果以点
轴上的点.如果以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则![]() 的坐标为__________.
的坐标为__________.
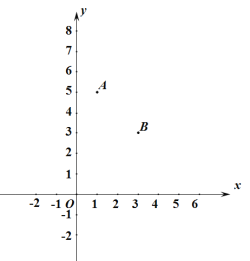
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
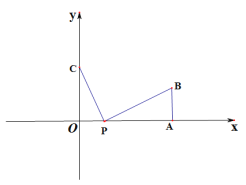
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com