
在平面直角坐标系中,已知二次函数 的图象与
的图象与 轴相交于点
轴相交于点 ,顶点为
,顶点为 ,点
,点 在这个二次函数图象的对称轴上.若四边形
在这个二次函数图象的对称轴上.若四边形 是一个边长为2且有一个内角为
是一个边长为2且有一个内角为 的菱形.求此二次函数的表达式.
的菱形.求此二次函数的表达式.
y=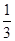 (x-1)2-1;y=
(x-1)2-1;y=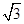 (x-1)2-
(x-1)2-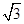 ;y=-
;y=-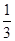 (x-1)2+1;y=-
(x-1)2+1;y=-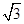 (x-1)2+
(x-1)2+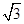 .
.
解析试题分析:根据题意,画出图形,可得以下四种情况:
(1)以菱形长对角线两顶点作为A、B,且抛物线开口向上;
(2)以菱形长对角线两顶点作为A、B,且抛物线开口向下;
(3)以菱形短对角线两顶点作为A、B,且抛物线开口向上;
(4)以菱形短对角线两顶点作为A、B,且抛物线开口向下,
解答时都利用四边形ACBD是一个边长为2且有一个内角为60°的条件根据解直角三角形的相关知识解答.
本题共有4种情况.
设二次函数的图象的对称轴与x轴相交于点E.
(1)如图①,
当∠CAD=60°时,
因为ACBD是菱形,一边长为2,
所以DE=1,BE=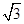 ,
,
所以点D的坐标(1,1),点C的坐标为(1,-1),
解得k=-1,a=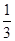 .
.
所以y=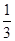 (x-1)2-1.
(x-1)2-1.
(2)如图②,当∠ACB=60°时,由菱形性质知点A的坐标为(0,0),点C的坐标为(1,-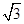 ).
).
解得k=-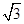 ,a=
,a=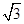 ,
,
所以y=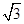 (x-1)2-
(x-1)2-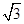 .
.
同理可得:y=-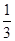 (x-1)2+1,y=-
(x-1)2+1,y=-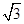 (x-1)2+
(x-1)2+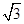 .
.
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
某水果店销售某中水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2﹣8mx+n,其变化趋势如图2.
(1)求y2的解析式;
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,A是抛物线 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当 时,求S的值.
时,求S的值.
(2)求S关于 的函数解析式.
的函数解析式.
(3)①若S= 时,求
时,求 的值;
的值;
②当m>2时,设 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一个二次函数的关系式为 y=x2-2bx+c.
(1)若该二次函数的图象与x轴只有一个交点,
①则b、c 应满足关系为 ;
②若该二次函数的图象经过A(m,n)、B(m +6,n)两点,求n的值;
(2)若该二次函数的图象与x轴有两个交点C(6,0)、D(k,0),线段CD(含端点)上有若干个横坐标为整数的点,且这些点的横坐标之和为21,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供了如下两个信息图,如甲、乙两图。
注:甲、乙两图中的A、B、C、D、E、F、G、H所对应的纵坐标分别指相应月份每千克该种蔬菜的售价和成本(生产成本6月份最低,甲图的图象是线段,乙图的图象是抛物线的一部分)。请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?最大收益是多少?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m),
(1)求二次函数的解析式并写出D点坐标;
(2)点Q是线段AB上的一动点,过点Q作QE∥AD交BD于E,连结DQ,当△DQE的面积最大时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与 轴相切于点C,与
轴相切于点C,与 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线 经过A,B,C三点.
经过A,B,C三点.
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,已知二次函数的图像经过原点及点A(1,2),与x轴相交于另一点B(3,0),将点B向右平移3个单位得点C.
(1)求二次函数的解析式;
(2)点M在线段OC上,平面内有一点Q,使得四边形ABMQ为菱形,求点M坐标;
(3)点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D、点E、点F也随之运动);
①当点E在二次函数的图像上时,求OP的长;
②若点P从O点出发向C点做匀速运动,速度为每秒1个单位长度,若P点运动t秒时,直线AC与以DE为直径的⊙M相切,直接写出此刻t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com