
 交y轴于点A.抛物线
交y轴于点A.抛物线 的图象过点E(-1,0),并与直线l相交于A、B两点.
的图象过点E(-1,0),并与直线l相交于A、B两点.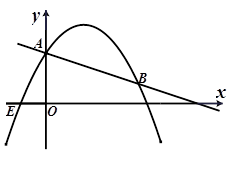
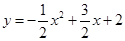
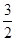 ,
,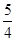 )
)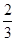 ,0),M2(
,0),M2(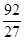 ,0),M3(
,0),M3(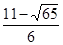 ,0),M4(
,0),M4(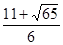 ,0)
,0) 交y轴于点A(0,2),
交y轴于点A(0,2), 上的点,
上的点,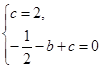 ,解得
,解得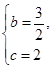 .
.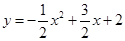 .
. 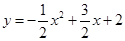 =
=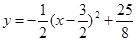 ,∴对称轴为x=
,∴对称轴为x=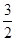 ,
, 的对称点为F(4,0).
的对称点为F(4,0).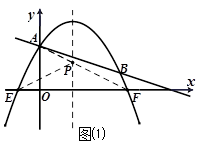
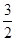 的交点即为所求P点,由于E、F两点关于对称轴对称,则此时△PAE的周长=PA+PE+AE
的交点即为所求P点,由于E、F两点关于对称轴对称,则此时△PAE的周长=PA+PE+AE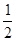 ,
,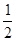 x+2.
x+2.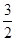 时,y=
时,y=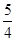 ,∴P点坐标为(
,∴P点坐标为(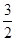 ,
,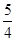 ).
). 交x轴于点C,令y=0,得x=6,∴C(6,0).
交x轴于点C,令y=0,得x=6,∴C(6,0).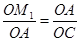 .
.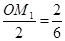 ,
,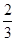 ,∴M1(-
,∴M1(-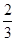 ,0).
,0). 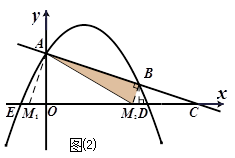
 和抛物线
和抛物线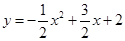 的交点,
的交点,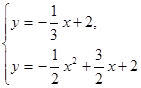 ,解得
,解得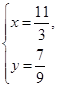 ,或
,或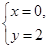 (舍)
(舍)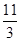 ,
,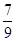 ).
).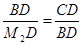 .
.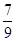 ,M2D=
,M2D=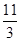 -m,CD=6-
-m,CD=6-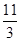 =
=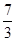 ,
,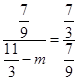 ,解得m=
,解得m=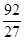 ,∴M2(
,∴M2(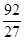 ,0).
,0).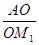 =3,
=3,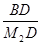 =
=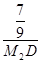 =3,
=3,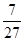 .∴OM2=OD-M2D=
.∴OM2=OD-M2D=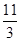 -
-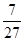 =
= ,
,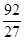 ,0).
,0).
 .
.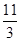 -t,OM=t,BD=
-t,OM=t,BD=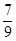 ,
,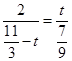 ,解得
,解得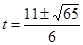 ,
,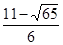 ,0),M4(
,0),M4(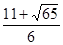 ,0).
,0).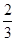 ,0),M2(
,0),M2(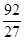 ,0),M3(
,0),M3(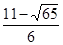 ,0),M4(
,0),M4(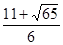 ,0).
,0).

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源:不详 题型:解答题
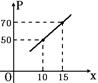
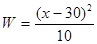 .在推广20cm~40cm的隔热瓦时,厂家进行市场营销,这种规格的隔热瓦广告费为每片10元.要使每片隔热瓦的利润不低于60.4元,求5cm~60cm的隔热瓦边长x的取值范围(x取整数).
.在推广20cm~40cm的隔热瓦时,厂家进行市场营销,这种规格的隔热瓦广告费为每片10元.要使每片隔热瓦的利润不低于60.4元,求5cm~60cm的隔热瓦边长x的取值范围(x取整数).查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A.y=- x2+x x2+x | B.y=-x2+x | C.y=- x2-x x2-x | D.y= x2-x x2-x |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
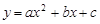 的图象与x轴交于(
的图象与x轴交于(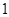 ,0)和(
,0)和(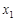 ,0),其中
,0),其中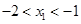 ,与
,与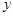 轴交于正半轴上一点.下列结论:①
轴交于正半轴上一点.下列结论:①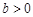 ;②
;②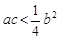 ;③
;③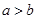 ;④
;④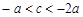 .其中所有正确结论的序号是_______.
.其中所有正确结论的序号是_______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com