[题目]如图.扇形纸扇完全打开后.阴影部分为贴纸.外侧两竹条AB.AC的夹角为120°.弧BC的长为30πcm.AD的长为15cm.则贴纸的面积等于cm2 ．题目和参考答案——青夏教育精英家教网—

【题目】如图，扇形纸扇完全打开后，阴影部分为贴纸，外侧两竹条AB，AC的夹角为120°，弧BC的长为30πcm，AD的长为15cm，则贴纸的面积等于cm2 ．

【答案】600π
【解析】解：∵弧BC的长为30πcm， ∴ =30π，
解得AB=45cm，
贴纸的面积=大扇形的面积﹣小扇形的面积，
= ×30π×45﹣ × ×15=600πcm2 ，
所以答案是600π．
【考点精析】利用弧长计算公式和扇形面积计算公式对题目进行判断即可得到答案，需要熟知若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】为了提高天然气使用效率,保障居民的本机用气需求,某地积极推进阶梯式气价改革,若一户居民的年用气量不超过300m3,价格为2.5元/m3,若年用气量超过300m3,超出部分的价格为3元/m3，

（1）根据题意,填写下表:

（2）设一户居民的年用气量为xm3,付款金额为y元,求y关于x的解析式;

（3）若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.

查看答案和解析>>

科目：初中数学 来源： 题型：

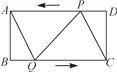
【题目】如图，在矩形ABCD中，AB＝4 cm，BC＝8 cm，点P从点D出发向点A运动，运动到点A即停止；同时点Q从点B出发向点C运动，运动到点C即停止．点P，Q的速度的速度都是1 cm/s，连结PQ，AQ，CP，设点P，Q运动的时间为t(s)．

(1)当t为何值时，四边形ABQP是矩形？

(2)当t为何值时，四边形AQCP是菱形？

(3)分别求出(2)中菱形AQCP的周长和面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作;……依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形.如图1，平行四边形ABCD中，若AB=1，BC=2，则平行四边形ABCD为1阶准菱形.

（I）判断与推理：

（i）邻边长分别为2和3的平行四边形是_________阶准菱形；

（ii）为了剪去一个菱形，进行如下操作：如图2，把平行四边形ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE，请证明四边形ABFE是菱形.

（Ⅱ）操作与计算：

已知平行四边形ABCD的邻边长分别为l，a（a>1），且是3阶准菱形，请画出平行四边形ABCD及裁剪线的示意图，并在图形下方写出a的值.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，在直角坐标系中，有A（0，3），B（2，1），C（﹣3，﹣3）三点．

（1）请在平面直角坐标系中描出各点，并画出三角形ABC；

（2）三角形ABC的面积是　　；（直接写出结果）

（3）设BC交y轴于点P，试求P点的坐标．

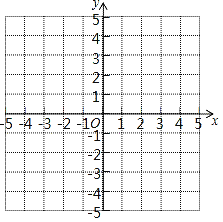
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，BD⊥AC，垂足为D，AB=AC=9，BC=6，求BD的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：△ABC内接于⊙O，过点A作直线EF．
（1）如图①，AB为直径，要使EF为⊙O的切线，还需添加的条件是（只需写出三种情况）： ①；②；③ ．
（2）如图②，AB是非直径的弦，∠CAE=∠B，求证：EF是⊙O的切线．
（3）如图③，AB是非直径的弦，∠CAE=∠ABC，EF还是⊙O的切线吗？若是，请说明理由；若不是，请解释原因．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系xoy中，直线y=x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C，点D是抛物线的顶点．

（1）求此抛物线的解析式；
（2）点P是直线AB上方的抛物线上一点，（不与点A、B重合），过点P作x轴的垂线交x轴于点H，交直线AB于点F，作PG⊥AB于点G．求出△PFG的周长最大值；
（3）在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M，使得△ABM与△ABD的面积相等？若存在，请求出此时点M的坐标；若不存在，请说明理由．