

分析 (1)作BG⊥y轴于G,作CP⊥x轴于P,BG与CP交于H;由AAS证明△BCH≌△COP,得出对应边相等BH=CP=1,CH=OE=3,求出BG、HP即可;
(2)如图2,作辅助线,构建全等三角形,证明△OAD≌△OQD(AAS),得OA=OQ,再证明Rt△OQE≌Rt△OCE(HL),根据全等三角形的对应角相等可得∠DOE=45°;
(3)结论:$\sqrt{2}$MN=ON+NC,作辅助线,构建直角梯形,根据直角梯形的中位线定理得:MH=$\frac{1}{2}$(AG+CN),再证明△AOG≌△OCN,得AG=ON,由O、N、C、M四点共圆,可知∠ONM=∠OCM=45°,则△MHN是等腰直角三角形,所以MN=$\sqrt{2}$MH,代入可得结论.
解答 解:(1)作BG⊥y轴于G,作CP⊥x轴于P,BG与CP交于H,如图1,
则∠BHC=∠CPO=90°,
∴∠HBC+∠BCH=90°,
∵C点坐标为(3,1),
∴OP=3,CP=1,
∵四边形ABCO是正方形,
∴BC=OC,∠BCO=90°,
∴∠BCH+∠OCP=90°,
∴∠HBC=∠OCP,
在△BCH和△COP中,
$\left\{\begin{array}{l}{∠BHC=∠CPO}\\{∠HBC=∠OCP}\\{BC=OC}\end{array}\right.$,
∴△BCH≌△COP(AAS),
∴BH=CP=1,CH=OP=3,
∴BG=3-1=2,HP=3+1=4,
∴点B的坐标为:(2,4);
(2)如图2,过O作OQ⊥DE于Q,
∵四边形AOCB是正方形,
∴AB∥OC,∠A=∠OCB=∠AOC=90°,AO=OC,
∴∠ADO=∠DOC,
∵∠ODE=∠DOC,
∴∠ADO=∠ODE,
∵∠A=∠OQD=90°,OD=OD,
∴△OAD≌△OQD(AAS),
∴OA=OQ,∠AOD=∠DOQ,
∵OE=OE,
∴Rt△OQE≌Rt△OCE(HL),
∴∠QOE=∠COE,
∵∠AOC=90°,
∴∠AOD+∠DOQ+∠QOE+∠EOC=90°,
∴∠DOQ+∠QOE=45°,
即∠DOE=45°;
(3)结论:$\sqrt{2}$MN=ON+NC,理由是:
如图3,过M作MH⊥x轴于H,过A作AG⊥x轴于G,连接AC,则四边形AGNC是直角梯形,
在正方形ABCD中,
∵M是OB的中点,
∴AC过M点,
∴AM=MC,
∵AG∥MH∥CN,
∴GH=NH,
∴MH是直角梯形AGCN的中位线,
∴MH=$\frac{1}{2}$(AG+CN),
∵∠AOC=90°,
∴∠AOG+∠CON=90°,
∵∠AGO=∠ONC=90°,
∴∠GAO+∠AOG=90°,
∴∠CON=∠GAO,
∵AO=OC,
∴△AOG≌△OCN,
∴AG=ON,
∵∠ONC=∠OMC=90°,
∴∠ONC+∠OMC=180°,
∴O、N、C、M四点共圆,
∴∠ONM=∠OCM=45°,
∴△MHN是等腰直角三角形,
∴MN=$\sqrt{2}$MH,
∴$\sqrt{2}$MN=2MH=2×$\frac{1}{2}$(AG+CN)=AG+CN=ON+CN.
点评 本题是四边形的综合题,考查了正方形的性质、全等三角形的判定与性质、坐标与图形性质;熟练掌握正方形的性质和作辅助线构建三角形全等是本题的关键,并能进行推理论证与计算,使问题得以解决.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{{3\sqrt{34}}}{34}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.5 | B. | 3.5 | C. | 8.5或3.5 | D. | 8.3或3.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
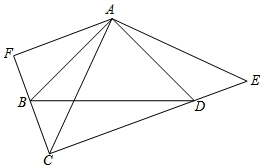 如图,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
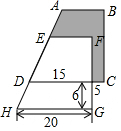 如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移的距离为线段AE的长,求阴影部分的面积.(单位:cm)
如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移的距离为线段AE的长,求阴影部分的面积.(单位:cm)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com