
分析 (1)根据有理数的加法,即可解答.
(2)根据有理数的减法,即可解答.
(3)先计算绝对值,再根据有理数的加法,即可解答.
(4)根据有理数混合运算,即可解答.
(5)根据有理数混合运算,即可解答.
(6)根据有理数混合运算,即可解答.
(7)根据有理数混合运算,即可解答.
(8)根据有理数混合运算,即可解答.
解答 解:(1)(-5)+12=7;
(2)(-5)-(+15)=-5-15=-20;
(3)-|-3|+(-$\frac{4}{5}$)=-3-$\frac{4}{5}$=-3$\frac{4}{5}$;
(4)-20+(-14)-(-18)-13=-20-14+18-13=-47+18=-29;
(5)-$\frac{2}{3}$+(+$\frac{5}{7}$)+(-$\frac{1}{3}$)+2$\frac{4}{7}$=-$\frac{2}{3}$$+\frac{5}{7}$-$\frac{1}{3}$+2$\frac{4}{7}$=-1+3$\frac{2}{7}$=2$\frac{2}{7}$;
(6)(-0.5)-(-3$\frac{1}{4}$)+2.75-(+7$\frac{1}{2}$)=-0.5+3$\frac{1}{4}$+2.75-7$\frac{1}{2}$=-8+6=-2;
(7)-20+(-14)-(-18)-13=-20-14+18-13=-47+18=-29;
(8)$\frac{2}{5}$-|-1$\frac{1}{2}$|-(+2$\frac{1}{4}$)-(-2.75)=$\frac{2}{5}$-1$\frac{1}{2}$-2$\frac{1}{4}$+2.75=$\frac{2}{5}-1$=-$\frac{3}{5}$.
点评 本题考查了有理数的混合运算,解决本题的关键是熟记有理数的混合运算顺序.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:填空题
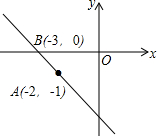 如图,直线y=kx+b过A(-2,-1),B(-3,0)两点,则不等式$\frac{1}{2}$x≥kx+b且kx+b<0的解集x≥-2.
如图,直线y=kx+b过A(-2,-1),B(-3,0)两点,则不等式$\frac{1}{2}$x≥kx+b且kx+b<0的解集x≥-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ①③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=10}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=10}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
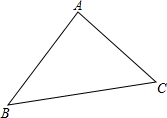 如图,在联欢晚会上,有A、B、C三名同学站在△ABC的三个顶点位置上,他们在玩抢凳子游戏,要求在△ABC内部放一个木凳,谁先抢到凳子谁获胜. 请在图中确定凳子应放的最适当的位置,使游戏公平.
如图,在联欢晚会上,有A、B、C三名同学站在△ABC的三个顶点位置上,他们在玩抢凳子游戏,要求在△ABC内部放一个木凳,谁先抢到凳子谁获胜. 请在图中确定凳子应放的最适当的位置,使游戏公平.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com